Démonstration par l'absurde d'unemoyenne de suite arithmétiq
15 messages
- Page 1 sur 1
démonstration par l'absurde d'unemoyenne de suite arithmétiq
Bonjour tout le monde
Quelqu'un peut-il m'aider à finaliser cette démonstration par l'absurde?
Voici une partie de mon travail cliquer ici: URL=http://www3.sympatico.ca/mmillery/qmath.htm]question Math[/URL]
Merci déjà pour votre aide.
Quelqu'un peut-il m'aider à finaliser cette démonstration par l'absurde?
Voici une partie de mon travail cliquer ici: URL=http://www3.sympatico.ca/mmillery/qmath.htm]question Math[/URL]
Merci déjà pour votre aide.
le lien
Il semble qu'il y eu une erreur dans le lien
Voici le lien
http://www3.sympatico.ca/mmillery/qmath.htm
Voici le lien
http://www3.sympatico.ca/mmillery/qmath.htm
permettez moi de faire irruption pour dire que:
La proposition est fausse car si je prends l'ensemble de valeur suivant:
{3;3;3;3;3;3;3;3;3;3}
La moyenne est 3
et si je prend une valeur moins la moyenne, je ne trouve pas qqch de strictement positif ....
ou est mon incomprehension ?
- La proposition pour moi est fausse
- Je comprend pas ton raisonnement Tize
La proposition est fausse car si je prends l'ensemble de valeur suivant:
{3;3;3;3;3;3;3;3;3;3}
La moyenne est 3
et si je prend une valeur moins la moyenne, je ne trouve pas qqch de strictement positif ....
ou est mon incomprehension ?
Flodelarab a écrit:Oui mais la proposition de départ est absurde.
d'ailleurs, c pas ça un raisonnement par l'absurde.
un raisonnement par l'absurde est un peu comme la contreapposée.
Je ne veux pas trop m'etendre sur ce genre de pb...mais après
tize a écrit:Je ne veux pas trop m'etendre sur ce genre de pb...mais aprèson divise par n et on a :
ce qui est absurde d'ou l'existence de i tel que
Moi non plus je veux pas m'etendre sur ce probleme.
un seul contre exemple suffit a montrer qu'une proposition est fausse.
Je repete donc :
La proposition est fausse si je prends l'ensemble de valeur suivant:
{3;3;3;3;3;3;3;3;3;3}
La moyenne est 3
et si je prend une valeur moins la moyenne, je ne trouve pas qqch de strictement positif ....
alben a écrit:Bonjour Flodelarab
Alors on s'emmêle les crayons ? :we:
Tu affirmes que la proposition est fausse. Tu as raison. Et comme c'est l'hypothèse du raisonnement par l'absurde, cela veut dire que la propostion initiale est vraie !
Bravo tu es donc d'accord à 100 % avec tize
Aaaa
je comprend mieux, Flodelarab voulait dire que c'est ma proposition de depart qui est fausse et non pas celle de henmil...ba oui c'est normal comme l'a expliqué alben... :we:
alors j'écris en clair et en entier mon idée
pouf pouf
on veut démontrer: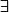 i
i  {1,
., n} | xi
{1,
., n} | xi 
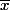 =>
=> 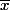 - xi > 0
- xi > 0
Notre ami nous propose l'absurde. Soit! Mais la proposition a la base est fausse.
je prend {3;3}
la moyenne est 3
je peux trouver un élément (3) qui vérifie xi
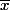 puisque
puisque 
par contre 3-3 n'est pas strictement supérieur a 0 donc xi -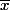 n'est pas supérieur strictement donc la proposition initiale est fausse.
n'est pas supérieur strictement donc la proposition initiale est fausse.
partant de la, le faux permet de tout démontrer ...
le raisonnement que nous propose henmil n'est donc pas par l'absurde mais absurde
est on d'accord ?
pouf pouf
on veut démontrer:
Notre ami nous propose l'absurde. Soit! Mais la proposition a la base est fausse.
je prend {3;3}
la moyenne est 3
je peux trouver un élément (3) qui vérifie xi
par contre 3-3 n'est pas strictement supérieur a 0 donc xi -
partant de la, le faux permet de tout démontrer ...
le raisonnement que nous propose henmil n'est donc pas par l'absurde mais absurde
est on d'accord ?
Flodelarab a écrit:alors j'écris en clair et en entier mon idée
pouf pouf
on veut démontrer:i
{1, ., n} | xi

=>
- xi > 0
Notre ami nous propose l'absurde. Soit! Mais la proposition a la base est fausse.
je prend {3;3}
la moyenne est 3
je peux trouver un élément (3) qui vérifie xi
puisque

par contre 3-3 n'est pas strictement supérieur a 0 donc xi -n'est pas supérieur strictement donc la proposition initiale est fausse.
partant de la, le faux permet de tout démontrer ...
le raisonnement que nous propose henmil n'est donc pas par l'absurde mais absurde
est on d'accord ?
non non c'est =>
15 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 74 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
