Encadrement/Majoration Intégrale
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
AdrienM07
- Messages: 4
- Enregistré le: 16 Sep 2016, 19:01
-
 par AdrienM07 » 16 Sep 2016, 19:33
par AdrienM07 » 16 Sep 2016, 19:33
Enoncer :
"3)Majoration des intégrales.
1) Montrer, en encadrant l'intégrale que
Pour tous x >0
 \leq \exp (-x^2) \times \int_{0}^{x}{\exp(t^2)}dt\leq x)
Attention : Cette intégrale ne se calcule pas
"
Bonjour je bloque sur cette question , c'est j'ai bien compris il faut chercher:
f(x) et g(x) tel que :
f(x)

)

g(x)

}\leq\int_{0}^{x}{\exp(t^2)}dt\leq \int_{0}^{x}{g(x)})
 \leq \exp (-x^2) \times \int_{0}^{x}{\exp(t^2)}dt\leq x)
Si c'est bien cela il me parait bien dure de trouver f(x) et g(x)
Quelqu'un pourrait-il me donner une piste ?

Cordialement
-
samoufar
- Membre Relatif
- Messages: 401
- Enregistré le: 28 Mai 2016, 17:43
- Localisation: Palaiseau
-
 par samoufar » 16 Sep 2016, 19:38
par samoufar » 16 Sep 2016, 19:38
Bonsoir,
Que dire de la monotonie de

sur
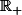
?
Que dire de l'intégrale d'une fonction monotone ?
Après, la majoration/minoration est simple, il ne faut pas chercher trop loin

-
AdrienM07
- Messages: 4
- Enregistré le: 16 Sep 2016, 19:01
-
 par AdrienM07 » 16 Sep 2016, 19:56
par AdrienM07 » 16 Sep 2016, 19:56
samoufar a écrit:Bonsoir,
Que dire de la monotonie de

sur
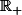
?
Que dire de l'intégrale d'une fonction monotone ?
Après, la majoration/minoration est simple, il ne faut pas chercher trop loin

hum
la fonction f(t) =
)
est strictement croissante sur R+
Après ton autre question me laisse perplexe

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 16 Sep 2016, 22:07
par zygomatique » 16 Sep 2016, 22:07
salut
et si tu multipliais les trois membres de l'inégalité par exp(t^2) ...
Rap ::
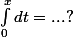
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
samoufar
- Membre Relatif
- Messages: 401
- Enregistré le: 28 Mai 2016, 17:43
- Localisation: Palaiseau
-
 par samoufar » 17 Sep 2016, 11:39
par samoufar » 17 Sep 2016, 11:39
Bonjour,
Pour ma deuxième question, elle devait te mettre sur la voie : l'intégrale d'une fonction croissante est croissante.
Par quoi peut-on encadrer

(ne cherches pas trop loin). Après tu peux passer à l'intégrale (c'est le but de ma deuxième question) et voir ce que ça donne

Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 55 invités
