Recherche d un PGCD et équation
40 messages
- Page 2 sur 2 - 1, 2
Re: recherche d un PGCD et équation
Allez, encore un exemple: quelles sont les solutions (x,y)=(4a,90-5a) telles que le PGCD de x et y soit égal à 90 ?
4a et 5a doivent être multiples de 90 donc a est de la forme 90m
(4a,90-5a)=(360m,90-450m)
Pour que le PGCD de x et y soit égal à 90, il faut que 4m et 1-5m soit premiers entre eux
soit 4m et 1-m soient premiers entre eux.
Comme m et 1-m sont premiers entre eux, il suffit que m soit pair (m=2n)
Les solutions sont (720n, 90-900n) avec n entier
par exemple avec n=1
(x,y)=(720,-810)
on a bien 5*720+4(-810)=360
et pgcd(720,-810)=90
4a et 5a doivent être multiples de 90 donc a est de la forme 90m
(4a,90-5a)=(360m,90-450m)
Pour que le PGCD de x et y soit égal à 90, il faut que 4m et 1-5m soit premiers entre eux
soit 4m et 1-m soient premiers entre eux.
Comme m et 1-m sont premiers entre eux, il suffit que m soit pair (m=2n)
Les solutions sont (720n, 90-900n) avec n entier
par exemple avec n=1
(x,y)=(720,-810)
on a bien 5*720+4(-810)=360
et pgcd(720,-810)=90
Re: recherche d un PGCD et équation
Je viens de réagir à un truc concon auquel j'avais jamais fait gaffe :
Pour résoudre dans l'équation
l'équation  avec
avec  entiers connus tels que
entiers connus tels que =1) donc tels qu'il existe
donc tels qu'il existe  vérifiant
vérifiant 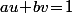 on peut écrire que :
on peut écrire que :

Et on retrouve évidement le résultat classique disant que les solutions sont données par mais on a aussi une relation un peu moins classique, à savoir que
mais on a aussi une relation un peu moins classique, à savoir que 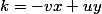 (relation qu'on peut parfaitement démontrer "à la main" en remplaçant
(relation qu'on peut parfaitement démontrer "à la main" en remplaçant  et
et  par leurs expressions).
par leurs expressions).
Cela montre que, non seulement et
et  sont combinaisons linéaires à coeffs. entiers de
sont combinaisons linéaires à coeffs. entiers de  et
et  , mais que réciproquement,
, mais que réciproquement,  et
et  sont combinaisons linéaires à coeffs. entiers de
sont combinaisons linéaires à coeffs. entiers de  et de
et de  et donc qu'on a systématiquement
et donc qu'on a systématiquement \!=\!\text{pgcd}(k,c))
Pour résoudre dans
Et on retrouve évidement le résultat classique disant que les solutions sont données par
Cela montre que, non seulement
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: recherche d un PGCD et équation
Salut Ben314
c est un résultat très intéressant mais j aime bien comprendre comment tu as trouvé la relation -vx+uy=k puis donner moi une démonstration
tu as commencer a cher une solution particulière au+bv=1 puis multiplier par c d ou a(cv)+b(cu)=c puis j n arrive pas a comprendre comment le signe - est obtenu et la relation -vx+uy=k ( et l existence du k )
svp donner votre démonstration et les étapes ( comment tu as eu l idée)
pour que l équation ax+by=c si on pose PGCD(a,b)=d 1er cas si d=1 il y a toujours des solutions quelque soit c
2 em cas si d différent de 1 il y a deux sous cas a) si c est un multiple de PGCD(a,b)=d l équation admet une solution
b)si c n est pas multiple de PGCD(a,b)=d l équation n admet pas de solution
svp pourquoi tu as pris un cas particulier PGCD(a,b)=1 peut on prendre un cas générale PGCD(a,b)=d et utiliser votre méthode
pour comment écrire le système et les formes des solutions et est ce qu on toujours PGCD(x,y)=PGCD(k,c)
aussi je n est pas compris l équivalence et l existence d un entier k t.q ...
donc on peut utiliser directement ce résultat par exemple
pour PGCD(x,y)=45 cela revient a chercher PGCD(k,360)=45
merci
c est un résultat très intéressant mais j aime bien comprendre comment tu as trouvé la relation -vx+uy=k puis donner moi une démonstration
tu as commencer a cher une solution particulière au+bv=1 puis multiplier par c d ou a(cv)+b(cu)=c puis j n arrive pas a comprendre comment le signe - est obtenu et la relation -vx+uy=k ( et l existence du k )
svp donner votre démonstration et les étapes ( comment tu as eu l idée)
pour que l équation ax+by=c si on pose PGCD(a,b)=d 1er cas si d=1 il y a toujours des solutions quelque soit c
2 em cas si d différent de 1 il y a deux sous cas a) si c est un multiple de PGCD(a,b)=d l équation admet une solution
b)si c n est pas multiple de PGCD(a,b)=d l équation n admet pas de solution
svp pourquoi tu as pris un cas particulier PGCD(a,b)=1 peut on prendre un cas générale PGCD(a,b)=d et utiliser votre méthode
pour comment écrire le système et les formes des solutions et est ce qu on toujours PGCD(x,y)=PGCD(k,c)
aussi je n est pas compris l équivalence et l existence d un entier k t.q ...
donc on peut utiliser directement ce résultat par exemple
pour PGCD(x,y)=45 cela revient a chercher PGCD(k,360)=45
merci
Re: recherche d un PGCD et équation
Salut Ben314
merci pour votre dernier message
svp donner moi plus d explication sur votre dernier message et méthode de recherche
comment démontrer le résultat
merci
merci pour votre dernier message
svp donner moi plus d explication sur votre dernier message et méthode de recherche
comment démontrer le résultat
merci
Re: recherche d un PGCD et équation
Dans le cas général, lorsque tu as a résoudre (en nombres entiers) ax+by=c avec a,b,c connus, tu commence effectivement par poser d=pgcd(a,b) ce qui signifie que a=da' , b=db' avec pgcd(a',b')=1 donc l'équation s'écrit alors d(a'x+b'y)=c.
Donc si d ne divise pas c, il n'y a clairement pas de solutions et, si d divise c, l'équation équivaut à a'x+b'y=d/c (avec c/d entier) dans laquelle pgcd(a',b')=1.
BILAN : on se ramène systématiquement à une équation de forme ax+by=c avec pgcd(a,b)=1 même si elle n'est pas de cette forme au départ.
Ensuite, en restant "basique" (i.e. sans utiliser de matrices), comme pgcd(a,b)=1, on sait qu'il existe u,v tels que au+bv=1 (théorème de Bézout) et on peut écrire que :
ax+by=c <=> ax+by=c(au+bv) <=> b(y-cv)=a(cu-x)
Donc a divise b(y-cv) et, comme il est premier avec b, cela signifie qu'il divise y-cv (lemme de Gauss) et donc que y-cv=ka pour un certain entier relatif k, soit encore y=cv+ka.
L'équation s'écrit alors a(cu-x)=bka c'est à dire cu-x=kb soit encore x=cu-kb.
Donc les solution de l'équation sont x=cu-kb ; y=cv+ka avec k entier relatif (on pourrait évidement écrire x=cu+kb ; y=cv-ka en remplaçant k par -k vu que k est un entier relatif ssi -k est un entier relatif).
Arrivé à ce point là, on constate qu'on a -vx+uy=-v(cu-kb)+u(cv+ka)=(-vu+uv)c+(vb+au)k=k.
On en déduit que :
1) Si un entier d quelconque divise à la fois x et y alors il divise c=ax+by ainsi que k=-vx+uy.
2) Réciproquement, si d divise à la fois c et k alors il divise x=cu-kb ainsi que y=cv+ka
Et cela signifie que pgcd(x,y)=pgcd(k,c)
Application numérique : 5x+4y=360 -> a=5 ; b=4 ; c=360
Il n'y a rien à diviser vu que dès le départ pgcd(5,4)=1
au+bv=1 a (par exemple) pour solution u=1 ; v=-1
Les solutions sont donc x=cu-kb=360-4k ; y=cv+ka=-360+5k avec k entier relatif
Et on a systématiquement pgcd(x,y)=pgcd(k,360) donc déterminer les solutions telles que pgcd(x,y)=d revient très exactement à déterminer les k tels que pgcd(k,360)=d.
Donc si d ne divise pas c, il n'y a clairement pas de solutions et, si d divise c, l'équation équivaut à a'x+b'y=d/c (avec c/d entier) dans laquelle pgcd(a',b')=1.
BILAN : on se ramène systématiquement à une équation de forme ax+by=c avec pgcd(a,b)=1 même si elle n'est pas de cette forme au départ.
Ensuite, en restant "basique" (i.e. sans utiliser de matrices), comme pgcd(a,b)=1, on sait qu'il existe u,v tels que au+bv=1 (théorème de Bézout) et on peut écrire que :
ax+by=c <=> ax+by=c(au+bv) <=> b(y-cv)=a(cu-x)
Donc a divise b(y-cv) et, comme il est premier avec b, cela signifie qu'il divise y-cv (lemme de Gauss) et donc que y-cv=ka pour un certain entier relatif k, soit encore y=cv+ka.
L'équation s'écrit alors a(cu-x)=bka c'est à dire cu-x=kb soit encore x=cu-kb.
Donc les solution de l'équation sont x=cu-kb ; y=cv+ka avec k entier relatif (on pourrait évidement écrire x=cu+kb ; y=cv-ka en remplaçant k par -k vu que k est un entier relatif ssi -k est un entier relatif).
Arrivé à ce point là, on constate qu'on a -vx+uy=-v(cu-kb)+u(cv+ka)=(-vu+uv)c+(vb+au)k=k.
On en déduit que :
1) Si un entier d quelconque divise à la fois x et y alors il divise c=ax+by ainsi que k=-vx+uy.
2) Réciproquement, si d divise à la fois c et k alors il divise x=cu-kb ainsi que y=cv+ka
Et cela signifie que pgcd(x,y)=pgcd(k,c)
Application numérique : 5x+4y=360 -> a=5 ; b=4 ; c=360
Il n'y a rien à diviser vu que dès le départ pgcd(5,4)=1
au+bv=1 a (par exemple) pour solution u=1 ; v=-1
Les solutions sont donc x=cu-kb=360-4k ; y=cv+ka=-360+5k avec k entier relatif
Et on a systématiquement pgcd(x,y)=pgcd(k,360) donc déterminer les solutions telles que pgcd(x,y)=d revient très exactement à déterminer les k tels que pgcd(k,360)=d.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: recherche d un PGCD et équation
Salur Ben314
merci pour les explications qui sont très claire .
j ai essayé d utiliser une autre façon ( car on a pas encore répondu a la question avec les congruences )
étude du cas générale
si on pose pgcd(x,y)=d et x=d.u et y=d.v et c=d.s avec PGCD(u,v)=1
d ou l équation a x+b y=c devient a (du)+b(d v)=c si d divise c alors on aura au+b v=c/d=s l équation devient au+b v=s
d ou il reste a déterminer les solutions u et v qui sont premiers entre eux
comment déterminer u et v solution de l équation au+b v=s et que vérifier qu ils sont premiers entre eux pgcd (u,v)=1
exemple d application
5x+4y=360 et pgcd(x,y)=36
on pose x=36 u et y =36 v e PGCD(u,v)=1
on obtient 5u+4v=10
u= 2+4k et v=-5k
il reste à montrer que PGCD(u,v)=1 ? comment procéder
merci
merci pour les explications qui sont très claire .
j ai essayé d utiliser une autre façon ( car on a pas encore répondu a la question avec les congruences )
étude du cas générale
si on pose pgcd(x,y)=d et x=d.u et y=d.v et c=d.s avec PGCD(u,v)=1
d ou l équation a x+b y=c devient a (du)+b(d v)=c si d divise c alors on aura au+b v=c/d=s l équation devient au+b v=s
d ou il reste a déterminer les solutions u et v qui sont premiers entre eux
comment déterminer u et v solution de l équation au+b v=s et que vérifier qu ils sont premiers entre eux pgcd (u,v)=1
exemple d application
5x+4y=360 et pgcd(x,y)=36
on pose x=36 u et y =36 v e PGCD(u,v)=1
on obtient 5u+4v=10
u= 2+4k et v=-5k
il reste à montrer que PGCD(u,v)=1 ? comment procéder
merci
Re: recherche d un PGCD et équation
Il y a comme toujours plusieurs méthodes plus ou moins astucieuses (voire celles proposées par chan ci dessus par exemple), mais un truc qui marche systématiquement (mais qui bien sûr n'est pas toujours le plus rapide), c'est de "virer" un des deux k en faisant des divisions euclidiennes successives :
pgcd(u;v) = pgcd(2+4k ; -5k) = pgcd(2+4k ; -5k+(2+4k)) = pgcd(2-k ; 2+4k+4(2-k)) = pgcd(2-k ; 10)
donc pgcd(u;v)=1 ssi pgcd(2-k ; 10)=1
Après, on peut (si on veut...) traduire différemment le fait que pgcd(2-k ; 10)=1 , par exemple
a) En disant que ça signifie que pgcd(2-k,2)=1 et pgcd(2-k,5)=1 soit encore que 2-k n'est divisible ni par 2 ni par 5, donc que k doit être impair mais pas de la forme 5j+2.
b) En disant que 2-k doit être congru à 1 ou 3 ou 7 ou 9 modulo 10 donc que k doit être congru à 1 ou 9 ou 5 ou 3 modulo 10 c'est à dire que k doit être de la forme 10j+r avec r=1 ou 3 ou 5 ou 9.
Et il doit y avoir encore d'autres façons de l'écrire...
pgcd(u;v) = pgcd(2+4k ; -5k) = pgcd(2+4k ; -5k+(2+4k)) = pgcd(2-k ; 2+4k+4(2-k)) = pgcd(2-k ; 10)
donc pgcd(u;v)=1 ssi pgcd(2-k ; 10)=1
Après, on peut (si on veut...) traduire différemment le fait que pgcd(2-k ; 10)=1 , par exemple
a) En disant que ça signifie que pgcd(2-k,2)=1 et pgcd(2-k,5)=1 soit encore que 2-k n'est divisible ni par 2 ni par 5, donc que k doit être impair mais pas de la forme 5j+2.
b) En disant que 2-k doit être congru à 1 ou 3 ou 7 ou 9 modulo 10 donc que k doit être congru à 1 ou 9 ou 5 ou 3 modulo 10 c'est à dire que k doit être de la forme 10j+r avec r=1 ou 3 ou 5 ou 9.
Et il doit y avoir encore d'autres façons de l'écrire...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: recherche d un PGCD et équation
Salut Ben314
si possible de m expliquer les autres façons de l écrire ( combien il y a de façons)
aussi u et v avec leurs formes et les valeurs possible de x et y avec leurs formes finales
( donc on doit avoir 4 valeurs de k )
merci
si possible de m expliquer les autres façons de l écrire ( combien il y a de façons)
aussi u et v avec leurs formes et les valeurs possible de x et y avec leurs formes finales
( donc on doit avoir 4 valeurs de k )
merci
Re: recherche d un PGCD et équation
Y'a rien d'autre qui me vient comme truc simple, mais si tu veut absolument un autre truc (sans aucun intérêt mais parfaitement juste sur le plan mathématique) tu peut écrire que pgcd(k-2,10)=1 ssi il existe a et b tels que (k-2)a-10b=1 donc k doit être de la forme k=2+(10b+1)/a avec b entier quelconque et a qui divise 10b+1.
Et je risque pas de te dresser la liste de tout ce qu'on pourrait écrire vu qu'il y a évidement une infinité de trucs possibles (plus ou moins utiles...)
Et en ce qui concerne l'écriture de u, v ou de x,y en fonction de k, je pense que tu es assez grand pour faire toi même les substitutions.
Et je risque pas de te dresser la liste de tout ce qu'on pourrait écrire vu qu'il y a évidement une infinité de trucs possibles (plus ou moins utiles...)
Et en ce qui concerne l'écriture de u, v ou de x,y en fonction de k, je pense que tu es assez grand pour faire toi même les substitutions.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: recherche d un PGCD et équation
Salut Ben314
si possible de m expliquer comment utiliser les congruences sans utiliser pgcd(x,y)=pgcd(k,c)
soit l équation 5x+4y=360 dont les solutions sont (x=44 + 4k ; y=35 − 5k) k de z
déterminer les solutions de l équation tel que PGCD(x,y)=36
est ce que je peut écrire x=0 mod(36) et y=0 mod 36 (= congru)
puis je détermine la valeur de l entier k mais qu est ce qu il faut ajouter comme conditions pour ne pas un autre valeur du PGCD différente du 36 sachant que PGCD(x,y) appartient a l ensemble de diviseurs de 360
merci
si possible de m expliquer comment utiliser les congruences sans utiliser pgcd(x,y)=pgcd(k,c)
soit l équation 5x+4y=360 dont les solutions sont (x=44 + 4k ; y=35 − 5k) k de z
déterminer les solutions de l équation tel que PGCD(x,y)=36
est ce que je peut écrire x=0 mod(36) et y=0 mod 36 (= congru)
puis je détermine la valeur de l entier k mais qu est ce qu il faut ajouter comme conditions pour ne pas un autre valeur du PGCD différente du 36 sachant que PGCD(x,y) appartient a l ensemble de diviseurs de 360
merci
Re: recherche d un PGCD et équation
Salut
Ben a fait largement le tour du sujet mais j'essaie encore une explication.
Il s'agit de déterminer les entiers k tels que:
PGCD(44+4k,35-5k)=36
il est "nécessaire" que et
et  soient congrus à 0 modulo 36.
soient congrus à 0 modulo 36.
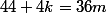 s'écrit
s'écrit 
soit
k=7+9m
D'autre part 35-5k=35-5(7+9m)=-45m
-45m doit être un multiple de 36
m doit être un multiple de 4
m=4n
k doit être de la forme 7+9m=7+9*4n=7+36n
(44+4k,35-5k)=(72+144n,-180n)
Pour que 36 soit effectivement le PGCD, il faut que (après division par 36),
le PGCD de (2+4n,-5n) soit égal à 1
(2(1+2n),-5n)
2 et 5 sont premiers entre eux, de même que 1+2n et n
on voit que n doit être impair
et il ne faut pas que




les solutions sont (72+144n,-180n) avec n impair et non congru à 2 modulo 5
Ben a fait largement le tour du sujet mais j'essaie encore une explication.
Il s'agit de déterminer les entiers k tels que:
PGCD(44+4k,35-5k)=36
il est "nécessaire" que
soit
k=7+9m
D'autre part 35-5k=35-5(7+9m)=-45m
-45m doit être un multiple de 36
m doit être un multiple de 4
m=4n
k doit être de la forme 7+9m=7+9*4n=7+36n
(44+4k,35-5k)=(72+144n,-180n)
Pour que 36 soit effectivement le PGCD, il faut que (après division par 36),
le PGCD de (2+4n,-5n) soit égal à 1
(2(1+2n),-5n)
2 et 5 sont premiers entre eux, de même que 1+2n et n
on voit que n doit être impair
et il ne faut pas que
les solutions sont (72+144n,-180n) avec n impair et non congru à 2 modulo 5
Re: recherche d un PGCD et équation
Salut chan79
merci beaucoup pour tes explications
c est cette méthode que j aime bien comprendre svp car la question demande d utiliser les congruences
d après votre réponse
on a 360=2^3.3^2.5=36 .2.5=36.10
PGCD(x,y)=36 équivaut que x et y sont divisibles par 36 Pour que 36 soit effectivement le PGCD, il faut que x et y ne soient pas divisibles par 10
en écriture de congruence x=0 mod 36 et y=0 mod 36 et x= p mod 10 avec 1<=p<=9 ( 1 ou 2ou3ou4ou5ou6ou7ou8ou9)
est possible de me vérifier ma réponse
pour un autre cas PGCD(x,y)=2 il faut écrire x et y sont divisibles par 2 et x et y non divisibles par 4 et 9 et 5)(il suffit non divisibles par 4,3 et 5 car 9 multiple de 3
pour un autre cas PGCD(x,y)=3 il faut écrire x et y sont divisibles par 3 et x et y non divisibles par 2 et4 et 9 t 5)(il suffit non divisibles par 2 et 5 car 4 multiple de 2 et 9 multiple de 3
comment écrie ça avec les congruences
merci
merci beaucoup pour tes explications
c est cette méthode que j aime bien comprendre svp car la question demande d utiliser les congruences
d après votre réponse
on a 360=2^3.3^2.5=36 .2.5=36.10
PGCD(x,y)=36 équivaut que x et y sont divisibles par 36 Pour que 36 soit effectivement le PGCD, il faut que x et y ne soient pas divisibles par 10
en écriture de congruence x=0 mod 36 et y=0 mod 36 et x= p mod 10 avec 1<=p<=9 ( 1 ou 2ou3ou4ou5ou6ou7ou8ou9)
est possible de me vérifier ma réponse
pour un autre cas PGCD(x,y)=2 il faut écrire x et y sont divisibles par 2 et x et y non divisibles par 4 et 9 et 5)(il suffit non divisibles par 4,3 et 5 car 9 multiple de 3
pour un autre cas PGCD(x,y)=3 il faut écrire x et y sont divisibles par 3 et x et y non divisibles par 2 et4 et 9 t 5)(il suffit non divisibles par 2 et 5 car 4 multiple de 2 et 9 multiple de 3
comment écrie ça avec les congruences
merci
Re: recherche d un PGCD et équation
Retiens que d est PGCD de a et b signifie que d est un diviseur commun à a et b et que a/d et b/d sont premiers entre eux.
Re: recherche d un PGCD et équation
Salut chan79
merci pour votre réponse
mais je n est pas comment l exploiter votre remarque
mais je sais cette technique mais mon problème je n arrive pas a appliquer votre remarque dans le cas ou pgcd(x,y) =d ou x et y sont inconnues mais la valeur d est connu
et pour ne pas avoir une autre valeur autre que d car on a un ensemble de valeurs
comment faire dans le cas générale
x et y sont divisible par d et il ne sont pas divisible par ( qui voici mon blocage ) a partir de la décomposition en facteurs premiers de c= ou ax+by=c autrement les facteurs a éliminer tels que x et y ne soit pas divisible pas eux
prenons un exemple
ex1) pgcd(x,y) appartient a l ensemble des diviseurs 2^4.3^2.5 suivant { 1, 2, 4,8.3,5,6,9,10,16,15 20 etc ...............} car 4x+5y=2^4.3^2.5^2.7^3
déterminer les solutions de l équation tel que pgcd(x,y)=2 puis pgcd(x,y)=3 pgcd(x,y)=5
svp donner moi plus d explications et de détails
merci
merci pour votre réponse
mais je n est pas comment l exploiter votre remarque
mais je sais cette technique mais mon problème je n arrive pas a appliquer votre remarque dans le cas ou pgcd(x,y) =d ou x et y sont inconnues mais la valeur d est connu
et pour ne pas avoir une autre valeur autre que d car on a un ensemble de valeurs
comment faire dans le cas générale
x et y sont divisible par d et il ne sont pas divisible par ( qui voici mon blocage ) a partir de la décomposition en facteurs premiers de c= ou ax+by=c autrement les facteurs a éliminer tels que x et y ne soit pas divisible pas eux
prenons un exemple
ex1) pgcd(x,y) appartient a l ensemble des diviseurs 2^4.3^2.5 suivant { 1, 2, 4,8.3,5,6,9,10,16,15 20 etc ...............} car 4x+5y=2^4.3^2.5^2.7^3
déterminer les solutions de l équation tel que pgcd(x,y)=2 puis pgcd(x,y)=3 pgcd(x,y)=5
svp donner moi plus d explications et de détails
merci
Re: recherche d un PGCD et équation
Salut Ben314
merci beaucoup pour tes explications
ma question principale c est comment déterminer les conditions pour ne pas avoir un autre pgcd autre que celui demander
par exemple c=2^2.3^2.5=180
pgcd(x,y) appartient {1,2,3,6,4,9.18,36,10,15,20,30,45,60,90,180}
pgcd(x,y)=3 équivaut à x et y sont divisible par 3 et x et y ne sont pas divisibles par ??? c est ici mon blocage pour ne pas avoir un autre valeur et comment ensuite passer aux congruences
c est cette méthode que j aime bien comprendre svp car la question demande d utiliser les congruences
d après votre réponse
on a 360=2^3.3^2.5=36 .2.5=36.10
PGCD(x,y)=18 équivaut que x et y sont divisibles par 18 Pour que 18 soit effectivement le PGCD, il faut que x et y ne soient pas divisibles par quels autres entiers
en écriture de congruence x=0 mod 18 et y=0 mod 18 et x= p mod (n) avec 1<=p<=9 ( 1 ou 2ou3ou4ou5ou6ou7ou8ou9)
est possible de me vérifier ma réponse
pour un autre cas PGCD(x,y)=5 il faut écrire x et y sont divisibles par 5 et x et y non divisibles par par quels autres entiers)(il suffit non divisibles par ??
pour un autre cas PGCD(x,y)=3 il faut écrire x et y sont divisibles par 3 et x et y non divisibles par )(il suffit non divisibles par 2
comment écrie ça avec les congruences
merci
merci beaucoup pour tes explications
ma question principale c est comment déterminer les conditions pour ne pas avoir un autre pgcd autre que celui demander
par exemple c=2^2.3^2.5=180
pgcd(x,y) appartient {1,2,3,6,4,9.18,36,10,15,20,30,45,60,90,180}
pgcd(x,y)=3 équivaut à x et y sont divisible par 3 et x et y ne sont pas divisibles par ??? c est ici mon blocage pour ne pas avoir un autre valeur et comment ensuite passer aux congruences
c est cette méthode que j aime bien comprendre svp car la question demande d utiliser les congruences
d après votre réponse
on a 360=2^3.3^2.5=36 .2.5=36.10
PGCD(x,y)=18 équivaut que x et y sont divisibles par 18 Pour que 18 soit effectivement le PGCD, il faut que x et y ne soient pas divisibles par quels autres entiers
en écriture de congruence x=0 mod 18 et y=0 mod 18 et x= p mod (n) avec 1<=p<=9 ( 1 ou 2ou3ou4ou5ou6ou7ou8ou9)
est possible de me vérifier ma réponse
pour un autre cas PGCD(x,y)=5 il faut écrire x et y sont divisibles par 5 et x et y non divisibles par par quels autres entiers)(il suffit non divisibles par ??
pour un autre cas PGCD(x,y)=3 il faut écrire x et y sont divisibles par 3 et x et y non divisibles par )(il suffit non divisibles par 2
comment écrie ça avec les congruences
merci
Re: recherche d un PGCD et équation
A force, je sais vraiment plus quoi te répondre, donc je vais te poser une question :YASMIN2016 a écrit:Salut Ben314
si possible de m expliquer comment utiliser les congruences sans utiliser pgcd(x,y)=pgcd(k,c)
Tu répondrait quoi à un collégien qui te demande comme résoudre l'équation 3x+5=4 en utilisant les identités remarquables et sans retrancher 5 des deux cotés de l'équation ?
Pour moi, ta question est du "même tonneau" : Comment résoudre le problème sans utiliser les outils adaptés, mais en en utilisant d'autres pas adaptés ?
Et, bizarrement, j'ai pas la réponse.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: recherche d un PGCD et équation
YASMIN2016 a écrit:Salut chan79
déterminer les solutions de l équation tel que pgcd(x,y)=2
svp donner moi plus d explications et de détails
merci
on cherche les k tels que PGCD(44+4k,35-5k)=2
PGCD(44+4k,35-5k)=PGCD(44+4k,44+4k+35-5k)=PGCD(44+4k,79-k)=PGCD(44+4k+4(79-k),79-k)=PGCD(360,79-k)
2 divise 360
il faut que 2 divise 79-k
k doit être impair
k=2m+1
(360,79-k)=(360,78-2m)
on divise par 2
le PGCD de (180,39-m) doit être 1
m doit être pair sinon 2 serait un diviseur commun
m=2n
(180,39-m)=(180,39-2n)
180=2²*3²*5
c'est là qu'on peut utiliser les congruences
39-2n ne doit pas être congru à 0 modulo 3
39-2n ne doit pas être congru à 0 modulo 5
modulo 3:
39=2n
0=2n
n=0
modulo 5:
39-2n=0
2n=39
2n=4
n=2
Les solutions (x,y) dont le pgcd est 2 sont:
x=44+4(4n+1)=48+16n
y=35-5(4n+1)=30-20n
à condition que n ne soit pas congru à 0 modulo 3 (non multiple de 3) et ne soit pas non plus congru à 2 modulo 5
Quelques valeurs de n positives et solutions correspondantes:
pour n=1, (x,y)=(64,10)
pour n=4, (x,y)=(112,-50)
pour n=5, (x,y)=(128,-70)
pour n=8, (x,y)=(176,-130)
pour n=10, (x,y)=(208,-170)
Modifié en dernier par chan79 le 18 Jan 2016, 09:30, modifié 1 fois.
Re: recherche d un PGCD et équation
On peut noter une périodicité pour le PGCD:
le PGCD de (44+4k,35-5k) est égal au PGCD de (44+4(k+360),35-5(k+360))
Le PGCD est 360 si k=79 (modulo 360).
Si on veut savoir pour quelles valeurs de k le PGCD de (44+4k,35-5k) est égal à 36 (par exemple), on peut faire une petite routine.
On trouve que k doit être égal (modulo 360) à l'un des nombres de l'ensemble: {43;115;187;331}
le PGCD de (44+4k,35-5k) est égal au PGCD de (44+4(k+360),35-5(k+360))
Le PGCD est 360 si k=79 (modulo 360).
Si on veut savoir pour quelles valeurs de k le PGCD de (44+4k,35-5k) est égal à 36 (par exemple), on peut faire une petite routine.
On trouve que k doit être égal (modulo 360) à l'un des nombres de l'ensemble: {43;115;187;331}
Re: recherche d un PGCD et équation
Même si c'est sans doute pas très important:
pour chaque PGCD possible (à gauche), le nombre de valeurs de k correspondantes comprises entre 1 et 360.

Exemple: il y a 48 valeurs de k (entre 1 et 360) telles que le PGCD de (44+4k,35-5k) est égal à 2.
Peut-on dire ce qui suit ?
Etant donnée une solution) de l'équation
de l'équation 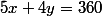 , la probabilité pour que
, la probabilité pour que  et
et  soient premiers entre eux est égale à
soient premiers entre eux est égale à  .
.
pour chaque PGCD possible (à gauche), le nombre de valeurs de k correspondantes comprises entre 1 et 360.

Exemple: il y a 48 valeurs de k (entre 1 et 360) telles que le PGCD de (44+4k,35-5k) est égal à 2.
Peut-on dire ce qui suit ?
Etant donnée une solution
40 messages
- Page 2 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 73 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
