Bonjour,
Je suis en plein révision, et je me suis arrêté sur un truc.
pgcd(a,b)=pgcd(a,b-a) comment le montrer ?
Ce qui vient à l'esprit :
soit d=pgcd(a,b) donc d divise a et b et d divise toute combinaison linéaire de a et b donc divise b-a.
soit d'=pgcd(a,b-a) donc d' divise a et b-a et d' divise toute combianison linéaire de a et b-a.
d et d' divisent a et b-a donc d=d'
Voila ma démo merci de signaler les éventuelles erreures
Pgcd(a,b)=pgcd(a,b-a)=pgcd(a,b-a)
7 messages
- Page 1 sur 1
Ton raisonnement est bon, tu as montré tout ce qu'il fallait mais ta conclusion est trop rapide. Je reprends ta démo:
Soit d=pgcd(a,b) et d'=pgcd(a,b-a)
d=pgcd(a,b) donc d divise a et b et d divise toute combinaison linéaire de a et b donc divise b-a donc d divise pgcd(a,b-a) donc d divise d'.
d'=pgcd(a,b-a) donc d' divise a et b-a et d' divise toute combinaison linéaire de a et b-a donc d' divise b donc pgcd(a,b) donc d' divise d.
Comme d divise d' et d' divise d et comme d et d' sont positifs alors d = d'
Soit d=pgcd(a,b) et d'=pgcd(a,b-a)
d=pgcd(a,b) donc d divise a et b et d divise toute combinaison linéaire de a et b donc divise b-a donc d divise pgcd(a,b-a) donc d divise d'.
d'=pgcd(a,b-a) donc d' divise a et b-a et d' divise toute combinaison linéaire de a et b-a donc d' divise b donc pgcd(a,b) donc d' divise d.
Comme d divise d' et d' divise d et comme d et d' sont positifs alors d = d'
Bonjour,
J'ai un petit problème, et j'aimerai bien avoir votre aide si c'est possible.
Voici l'enoncé :
1 - vérifier que 111 est divisible par 3.
2 - n désigne un entier naturel supérieur à 3.
 est le nombre dont l'écriture décimale est constituée uniquement de 1 :
est le nombre dont l'écriture décimale est constituée uniquement de 1 :
[center]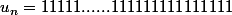 [/center]
[/center]
2a - Démontrer que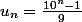
2b - Vérifier que pour tout réel a et b, :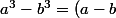(a^2+ab+b^2))
2c - Démontrer que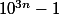 est divisible par
est divisible par 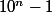
2d - En déduire que l'entier naturel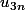 est divisible par l'entier naturel
est divisible par l'entier naturel 
2e - Démontrer que
2f - Démontrer que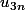 est divisible par
est divisible par 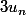
3 -Démontrer qu'il existe une infinité d'entiers naturels dont l'écriture décimale est constituée de exactement de n chiffres 1 et qui sont divisible par n.
[center] ---------- [/center]
1 -
a -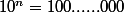 ,
,  ,
, 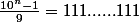
[CENTER]Donc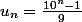 [/CENTER]
[/CENTER]
b -(a^2+ab+b^2)=a^3+a^2b+ab^2-a^2b-ab^2-b^3=a^3-b^3)
[CENTER]Donc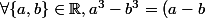(a^2+ab+b^2)) [/CENTER]
[/CENTER]
c -)
)
^3\equiv 1^3 (mod.\ 10^n-1))
)
[CENTER]
Donc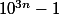 divise
divise 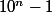 [/CENTER]
[/CENTER]
d -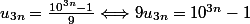 et
et 
 donc
donc 
[CENTER]Donc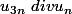 [/CENTER]
[/CENTER]
e - \Longleftrightarrow 10 \equiv 1 \(mod.\ 3)) Donc
Donc ) or
or 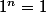
[CENTER]Donc) [/center]
[/center]
et
[CENTER]^2+10^n+1 \equiv 1^3+1+1 \equiv 3 \equiv 0 \ (mod. \ 3)) [/CENTER]
[/CENTER]
f - On veut montrer que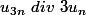
donc on peut déjà écrire :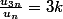
Donc}{(\frac{10^n-1}{9})}=\frac{10^{3n}-1}{10^n-1}=1à^{2n}+10^n+1)
Or)
[CENTER]Donc [/CENTER]
[/CENTER]
3 - je n'ai pas compris la question.
Merci de me corriger les éventuelles erreurs et me dire si ce que j'ai fait est bien ou nul
Merci
J'ai un petit problème, et j'aimerai bien avoir votre aide si c'est possible.
Voici l'enoncé :
1 - vérifier que 111 est divisible par 3.
2 - n désigne un entier naturel supérieur à 3.
[center]
2a - Démontrer que
2b - Vérifier que pour tout réel a et b, :
2c - Démontrer que
2d - En déduire que l'entier naturel
2e - Démontrer que
2f - Démontrer que
3 -Démontrer qu'il existe une infinité d'entiers naturels dont l'écriture décimale est constituée de exactement de n chiffres 1 et qui sont divisible par n.
[center] ---------- [/center]
1 -
a -
[CENTER]Donc
b -
[CENTER]Donc
c -
[CENTER]
Donc
d -
[CENTER]Donc
e -
[CENTER]Donc
et
[CENTER]
f - On veut montrer que
donc on peut déjà écrire :
Donc
Or
[CENTER]Donc
3 - je n'ai pas compris la question.
Merci de me corriger les éventuelles erreurs et me dire si ce que j'ai fait est bien ou nul
Merci
7 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 45 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
