Raisonnement par réccurence
19 messages
- Page 1 sur 1
raisonnement par réccurence
Bonjour, j'ai un peu de mal avec l'exo suivant, pouvez vous m'aider ?
On considère la suite (Un) définie par U0=1 et U(n+1)= 2Un -n+1
1) Montrer par récurrence que pour tout entier naturel Un > n
2) Montrer que (Un) est croissante
On considère la suite (Un) définie par U0=1 et U(n+1)= 2Un -n+1
1) Montrer par récurrence que pour tout entier naturel Un > n
2) Montrer que (Un) est croissante
bonjourbonsoir a écrit:mais pour l'hérédité on doit partir de U(n+1)>n+1 non ?
Pour montrer qu'une propriété est héréditaire on suppose qu'elle est vraie a un certain rang n et on montre qu'alors elle est aussi vraie au rang suivant (n+1).
Donc ici :
On suppose qu'il existe un n tel que U(n) > n
Et on montre qu'alors, U(n+1) est plus grand que n+1
On sait que U(n+1) = 2U(n) - n + 1
Si l'on suppose U(n) > n
alors 2U(n) > 2n (d'accord ? On a multiplié les 2 membres de l'inégalité par un nombre positif : 2)
et alors 2U(n) - n > 2n - n (d'accord ? On a ajouté -n des 2 côtés)
et alors 2U(n) - n + 1 > 2n - n + 1 (toujours d'accord ? On a ajouté 1 des 2 côtés)
Mais je te rappelle que 2U(n) - n +1 c'est U(n+1)
On a donc prouvé que si on a U(n) > n alors on a aussi U(n+1) > n+1
Si l'on suppose U(n) > n
alors 2U(n) > 2n (d'accord ? On a multiplié les 2 membres de l'inégalité par un nombre positif : 2)
et alors 2U(n) - n > 2n - n (d'accord ? On a ajouté -n des 2 côtés)
et alors 2U(n) - n + 1 > 2n - n + 1 (toujours d'accord ? On a ajouté 1 des 2 côtés)
Mais je te rappelle que 2U(n) - n +1 c'est U(n+1)
On a donc prouvé que si on a U(n) > n alors on a aussi U(n+1) > n+1
P'tipito t'explique le principe du raisonnement par récurrence :
- On démontre que la propriété est héréditaire , c'est à dire que si elle est vraie à un rang n alors elle est vraie au rang suivant. Autrement dit que (P(n) Vraie) entraine (P(n+1) Vraie)
- Puis on démontre qu'elle est vraie pour n=0 (initialisation)
On en déduit qu'elle est vraie pour n=1 (car vraie pour 0 donc vraie pour 1.
Et qu'elle est vraie pour n=2 (car vraie pour 1 donc vraie pour 2.
Et qu'elle est vraie pour n=3 (car vraie pour 2 donc vraie pour 3.
....
Et on peut alors conclure qu'elle est vraie pour tout n.
Ce que je t'ai donné, c'est la démonstration que la propriété est héréditaire :
- On démontre que la propriété est héréditaire , c'est à dire que si elle est vraie à un rang n alors elle est vraie au rang suivant. Autrement dit que (P(n) Vraie) entraine (P(n+1) Vraie)
- Puis on démontre qu'elle est vraie pour n=0 (initialisation)
On en déduit qu'elle est vraie pour n=1 (car vraie pour 0 donc vraie pour 1.
Et qu'elle est vraie pour n=2 (car vraie pour 1 donc vraie pour 2.
Et qu'elle est vraie pour n=3 (car vraie pour 2 donc vraie pour 3.
....
Et on peut alors conclure qu'elle est vraie pour tout n.
Ce que je t'ai donné, c'est la démonstration que la propriété est héréditaire :
Si l'on suppose U(n) > n
alors 2U(n) > 2n (d'accord ? On a multiplié les 2 membres de l'inégalité par un nombre positif : 2)
et alors 2U(n) - n > 2n - n (d'accord ? On a ajouté -n des 2 côtés)
et alors 2U(n) - n + 1 > 2n - n + 1 (toujours d'accord ? On a ajouté 1 des 2 côtés)
Mais je te rappelle que 2U(n) - n +1 c'est U(n+1)
On a donc prouvé que si on a U(n) > n alors on a aussi U(n+1) > n+1
analyse et synthèse
Quand on veut montrer que 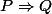 et que l'on ne trouve pas (!),
et que l'on ne trouve pas (!),
on part de Q et on cherche des conditions nécessaires à Q. On dit que c'est la phase d'analyse
si , on peut regarder ensuite (toujours dans la phase d'analyse)
, on peut regarder ensuite (toujours dans la phase d'analyse)
les rapports entre les propriétés P et R. Mais bon, dans la phase de synthèse,
on montre que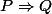 .
.
on part de Q et on cherche des conditions nécessaires à Q. On dit que c'est la phase d'analyse
si
les rapports entre les propriétés P et R. Mais bon, dans la phase de synthèse,
on montre que
P'tipito a écrit:Il y a meme pas besoin d'une recurrence ici. Il suffit d'ecrire u(n+1)-u(n) et d'utiliser la question 1.
Mais si tu as vraiment du mal avec le raisonnement par recurrence bonjourbonsoir, tu peux faire la 2 par recurrence pour t'entrainer
Certes on peut en effet utiliser cette approche mais il faudra alors démontrer que pour tout
19 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 142 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
