évaluer une integrale

[jehu73]

bonsoir,

je dois évaluer l'integrale suivante

Jk =;) Dx/(x²+1)^k k entier naturel

Merci pour votre aide

[WillyCagnes]

bsr
Dx=derivée de x? dx

soit f(x)=dx/(1+x²)^k
ou f(x)=1/(1+x²)^k

[jehu73]

Bonsoir Willy
La fonction est

f(x) =1/(1+x²)^k

[Kolis]

Bonjour !
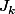
En calculant la dérivée de tu trouveras une relation entre et

[Black Jack]

bonsoir,

je dois évaluer l'integrale suivante

Jk =;) Dx/(x²+1)^k k entier naturel

Merci pour votre aide

Si c'est une intégrale, alors il manque les bornes d'intégration.

:zen:

[Abuche]

Cela dépend aussi de la forme attendu pour Jk.

1/(x^2+1)^k+1 =(x^2+1)/(..) - (x^2) /(..)

Suit Jk - Jk+1 = int ( x^2 / (x^2+1)^k+1 )

Par télescopage Jk est l'intégrale d'une série

[jehu73]

Il n y a pas de forme spécifié..donc je suppose la plus réduite ou plus simplifié

[Abuche]

Sans démarrage et un début, faut travailler plus :

x=tan(u) ira vers du cos(u) et une intégrale bien connue

[jehu73]

je sais que
;) 1/(1+x²)^1=arctang(x)
et que
;) 1/(1+x²)^2 = 1/2(x/(1+X²)+Arctang(x))

Apres j'ai du mal à faire une relation :hein:

[Kolis]

Je t'ai donné une méthode à 08h43 : as-tu essayé ?

[Abuche]

[jehu73]

Non jolis je n ai pas encore essayé. Je vois ça ce soir et je te donne mon résultat
Merci

[Abuche]

Cela mène vers du x^2/(x^2+1)^k , et la récurrence ne se simplifie pas
Avec le cos^k , calculer quelques termes donne une allure générale de la série
Ecrire la série avec le terme synthétique en k, je ne suis pas allé jusque là

.. Les icônes saturent et le forum aussi

[Kolis]

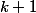
C'est plutôt que . Peu importe.

Le c'est donc
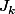
et on en déduit bien une formule de récurrence entre et

[jehu73]

voici ce que je trouve
Jk=;)1/(x²+1)^k-1 dx - ;)x²/(x²+1)^k dx
Jk=Jk-1 - ;)x²/(x²+1)^k dx

on fait une IPP au borne [0;+inf] car k entier naturel
Avec u(x)=x et v'(x)=x/(x²+1)^k

cela donne

Jk=Jk-1-(1/(2(k+1))*Jk+1

qu'en pensez vous?

[Kolis]

Sans les indices correctement placés je ne peux rien dire !

De toutes façons il manque le terme "tout intégré" :

[chan79]

Une intégration par parties donne:




avec

[jehu73]

pour l'ipp j'ai
u(x) =x u'(x) =1
v'(x) =x/(x²+1)^k v(x)=-1/(2(k+1)(x²+1)^k+1)

sachant que k est un entier naturel j'ai travaillé sur 0,+inf

Jk=Jk-1+[uv]-;)u'v
Jk=Jk-1+[0]+(1/(2(1-k))*Jk+1 le[uv]=0 car nous travaillons sur 0;+inf donc ca tend vers 0
et ;)u'v qui est =-1/(2(k+1)(x²+1)^k+1) se transforme en -(1/(2(1-k))*Jk+1
puisque -1/(x²+1)^k-1=-Jk+1 et que moins la primitive de -(1/(2(k+1) devient uniquement 1/(2(k+1))

donc

Jk=Jk-1-(1/(2(1-k))*Jk+1


si je n 'avais pas fait jouer les borne
Jk=Jk-1 - x/(2(k+1)(x²+1)^k+1) + 1/(2(1-k) * Jk+1


enfin je pense

[fibonacci]

Bonjour;

[fibonacci]

Suite