Difference entre évaluer une limite et une fonction

[spyrakos]

Bonjour,

J'ai du mal à voir la difference entre évaluer une fonction et une limite.
Je m'explique soit si j'évalue c'est exactement la même chose que .

Si je suis dans le cas d'une forme indéterminé comme
Je peux très bien faire la mise en évidence de pour simplifier la fraction, ce qui fera et donc évaluer par la suite . La simplification de la fonction lèvera l'indetermination.

[hdci]

Bonjour,

Vous avez raison dans le premier cas : c'est parce que la fonction est continue et définie en 3.

Pou le second cas, vous n'avez pas raison : -2 n'appartient pas au domaine de définition donc f(-2) n'existe pas. Par contre, la limite en -2 existe et vous pouvez "prolonger la fonction par continuité", en appelant la nouvelle fonction "f barre" et en disant que f barre est égale à f sur le domaine de définition de f, et pour laquelle l'image de -2 est 20.

Mais ce n'est pas toujours le cas : prenez la fonction "partie entière" : celle qui à x associe le plus grand entier inférieur ou égal à x. Notons-là E, et alors vous avez E(1)=1, mais E(0,9)=0, E(0,9999)=0, etc.
Ici, la fonction fait un "décrochage" en 1 : elle passe "instantanément" de 0 à 1, et il n'y a pas de limite en 1 (il y a une limite à droite, qui est 1, et une limite à gauche, qui est 0).

Autre cas de figure : considérez la fonction
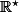
Vous voyez bien ici que le domaine de définition est , donc f(0) n'existe pas.
Et il n'y a pas moyen de factoriser par x pour faire disparaître ce dénominateur.

Pourtant, si vous utilisez un logiciel, une calculatrice, vous allez voir que la limite en zéro semble être égale à 1. Et c'est le cas en fait car quand x tend vers zéro, f(x) tend vers le nombre dérivé de l'exponentielle en zéro.

Enfin, dernier cas : supposons que je définisse pour x>0, et pour x<0 et . J'ai bien là une fonction définie sur mais qui n'a pas de limite en zéro, bien qu'ayant une image en zéro.