Bonjours,
Je dois évaluer l'intégral triple de xz+y^3, avec -1<=x<=1 0<=y<=2 0<=z<=1. Le résultat que j'obtiens est -8, est-ce normal que le volume soit négatif?
Merci de vos réponses.
évaluer une triple intégral
13 messages
- Page 1 sur 1
MTBB a écrit:Bonjours,
Je dois évaluer l'intégral triple de xz+y^3, avec -1<=x<=1 0<=y<=2 0<=z<=1. Le résultat que j'obtiens est -8, est-ce normal que le volume soit négatif?
Merci de vos réponses.
Comme ta fonction prend des valeurs négatives à certains endroits de ton domaine, il n'y a tien de choquant à ce que l'intégration puisse donner un résultat négatif.
Toutefois perso je trouve +8 comme résultat pour ton calcul. L'integration de xz donne 0 et celle de y^3 donne 2 x 1 x 2^4/4 = 8.
voici la question : Calculez l'aire de la partie du paraboloïde x=y^2+z^2 qui se trouve à l'intérieur du cylindre y^2+z^2=9
ma démarche:
j'ai déterminé que le rayon du cylindre étais de 3, le cercle d'intersection entre les 2 courbe est donc aussi de 3
j'ai modifier l'équation du cercle pour que mes coordonnées polaires soit selon le plan Oyz (r^2=y^2+z^2)
j'ai aussi modifier la formule d'air de surface polaire pour obtenir = \int\sqrt{1+\frac{dx}{dy}^2+\frac{dx}{dz}^2}dA)
le domaine d'intégration en polaire sera de
(le dA devient rdrd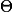 )
)
j'ai obtenue^{\frac{3}{2}}-1)}{6})
ma démarche:
j'ai déterminé que le rayon du cylindre étais de 3, le cercle d'intersection entre les 2 courbe est donc aussi de 3
j'ai modifier l'équation du cercle pour que mes coordonnées polaires soit selon le plan Oyz (r^2=y^2+z^2)
j'ai aussi modifier la formule d'air de surface polaire pour obtenir
le domaine d'intégration en polaire sera de
(le dA devient rdrd
j'ai obtenue
Hello,
Je ne comprends pas bien pourquoi tu passes en polaire.
Je suis d'accord pour la surface à considérer ( x <= 9 ) mais une fois que tu as ça tu as juste à intégrer le périmètre de tes cercles y^2+z^2 = x pour x entre 0 et 9. Le périmètre de chaque cercle est 2Pi racine(x), que tu intègres selon x entre 0 et 9 et Ca te donne 2Pi*3/2*9^(3/2) = 3Pi * 3^3 = 81Pi sauf erreur de calcul.
Pourquoi es-tu passé en polaire ? Meme si au final on devrait obtenir le Meme résultat.
Damien.
Je ne comprends pas bien pourquoi tu passes en polaire.
Je suis d'accord pour la surface à considérer ( x <= 9 ) mais une fois que tu as ça tu as juste à intégrer le périmètre de tes cercles y^2+z^2 = x pour x entre 0 et 9. Le périmètre de chaque cercle est 2Pi racine(x), que tu intègres selon x entre 0 et 9 et Ca te donne 2Pi*3/2*9^(3/2) = 3Pi * 3^3 = 81Pi sauf erreur de calcul.
Pourquoi es-tu passé en polaire ? Meme si au final on devrait obtenir le Meme résultat.
Damien.
ce que je cherche est l'air de la surface du paraboloïde , je peut soit utiliser =\int\int || \vec{r'_u} \wedge \vec{r'_v} ||dA) avec
avec  ,
, 
ou je peut utilisé la formule que j'ai envoyé plus tôt en polaire, je passe justement en polaire pour simplifier l'équation a intégrer
(la première formules est aussi une double intégral, je ne l'ai pas bien transcrit)
ou je peut utilisé la formule que j'ai envoyé plus tôt en polaire, je passe justement en polaire pour simplifier l'équation a intégrer
(la première formules est aussi une double intégral, je ne l'ai pas bien transcrit)
MTBB a écrit:ce que je cherche est l'air de la surface du paraboloïde , je peut soit utiliseravec
,
ou je peut utilisé la formule que j'ai envoyé plus tôt en polaire, je passe justement en polaire pour simplifier l'équation a intégrer
(la première formules est aussi une double intégral, je ne l'ai pas bien transcrit)
Au temps pour moi, je m'étais trompé sur ce coup là. Ton résultat m'a l'air bon.
13 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 40 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
