Bonjour, je suis en terminale S et je dois résoudre une équation dans ;) mais je bloque ... pouvez-vous m'aider s'il vous plaît ?
_
z + 2iRe(z) + 3 = Im(z) + 1 - i
Au début j'ai remplacé Re(z) par a et Im(z) par b mais après je ne sais pas comment faire ...
J'ai aussi essayé de remplacer 2iRe(z) par 2ia mais comme précédemment je suis bloquée ensuite ...
Merci d'avance !
Équations avec les nombres complexes
10 messages
- Page 1 sur 1
diabo a écrit:Bonjour, je suis en terminale S et je dois résoudre une équation dansmais je bloque ... pouvez-vous m'aider s'il vous plaît ?
z + 2iRe(z) + 3 = Im(z) + 1 - i
Au début j'ai remplacé Re(z) par a et Im(z) par b mais après je ne sais pas comment faire ...
J'ai aussi essayé de remplacer 2iRe(z) par 2ia mais comme précédemment je suis bloquée ensuite ...
Merci d'avance !
diabo a écrit:Bonjour, je suis en terminale S et je dois résoudre une équation dansmais je bloque ... pouvez-vous m'aider s'il vous plaît ?
_
z + 2iRe(z) + 3 = Im(z) + 1 - i
Au début j'ai remplacé Re(z) par a et Im(z) par b mais après je ne sais pas comment faire ...
J'ai aussi essayé de remplacer 2iRe(z) par 2ia mais comme précédemment je suis bloquée ensuite ...
Merci d'avance !
c'est une très bonne idée, ensuite sépare le bon grain de l'ivraie,ie, les parties réelles et imaginaires.
f(a,b)+i g(a,b)=0
avec f(a,b) et g(a,b) réelles
d'où f(a,b)=g(a,b)=0
salut
en notant z* le conjugué de z ...
 + 3 = Im(z) + 1 - i)
en prenant le conjugué
 + 3 = Im(z) + 1 + i)
car Re(z) et Im(z) sont des réels
donc en additionnant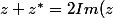 - 4) (1)
(1)
...
:zen:
or z + z* = 2Re(z) donc (1) a = b - 2 (en posant z = a + ib)
posons z = a + (a + 2)i
z* + 2iRe(z) + 3 = a - (a + 2)i + 2ia + 3 = a + 3 + (a - 2)i
Im(z) + 1 - i = a + 2 + 1 - i = a + 3 - i
donc a = 1
 .... j'ai corrigé les erreurs ....
.... j'ai corrigé les erreurs ....
en notant z* le conjugué de z ...
en prenant le conjugué
car Re(z) et Im(z) sont des réels
donc en additionnant
...
:zen:
or z + z* = 2Re(z) donc (1) a = b - 2 (en posant z = a + ib)
posons z = a + (a + 2)i
z* + 2iRe(z) + 3 = a - (a + 2)i + 2ia + 3 = a + 3 + (a - 2)i
Im(z) + 1 - i = a + 2 + 1 - i = a + 3 - i
donc a = 1
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Bonjour, merci pour toutes vos réponses mais je vous avoue que je n'ai toujours pas très bien compris ...
En fait lorsque je remplace Re(z) Im(z) et z* par a,b et a-ib je n'arrive pas à regrouper les termes de telle manière à trouver deux expressions de nombres complexes ?
Mathelot, je n'ai pas compris votre méthode nous n'avons pas vu ça en cours. Je vous met l'exemple du cours pour que vous voyiez comment nous avions procédé :
iz* = 2z + 2i
i(a-ib) = 2(a+ib) + 2i
b+ia = 2a + i(2+2b)
Puis on a résolu le système : b = 2a
a = 2 + 2b
Et la solution est S=-2/3 - (4/3)*i
En fait lorsque je remplace Re(z) Im(z) et z* par a,b et a-ib je n'arrive pas à regrouper les termes de telle manière à trouver deux expressions de nombres complexes ?
Mathelot, je n'ai pas compris votre méthode nous n'avons pas vu ça en cours. Je vous met l'exemple du cours pour que vous voyiez comment nous avions procédé :
iz* = 2z + 2i
i(a-ib) = 2(a+ib) + 2i
b+ia = 2a + i(2+2b)
Puis on a résolu le système : b = 2a
a = 2 + 2b
Et la solution est S=-2/3 - (4/3)*i
diabo a écrit:Bonjour, je suis en terminale S et je dois résoudre une équation dansmais je bloque ... pouvez-vous m'aider s'il vous plaît ?
_
z + 2iRe(z) + 3 = Im(z) + 1 - i (*)
Au début j'ai remplacé Re(z) par a et Im(z) par b mais après je ne sais pas comment faire ...
J'ai aussi essayé de remplacer 2iRe(z) par 2ia mais comme précédemment je suis bloquée ensuite ...
Merci d'avance !
posons z=x+iy
Dans l'égalité (*) , nous égalisons les parties réelles
x+3=y+1
Dans l'égalité (*) , nous égalisons les parties imaginaires (qui sont des réels)
-y+2x=-1
Nous obtenons un système de deux équations à deux inconnues:
10 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 46 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
