Bonsoir,
Se posent à moi aujourd'hui 2 questions :
-Si f est dérivable respectivement sur [0;1] et [1;2], est- elle dérivable sur [0;2] ? d'après le corrigé du livre non ... Je ne vois pas trop, il se peut que ce soit une erreur ou alors je ne comprends pas.
De plus j'ai trouvé sur internet quelqu'un qui disait (en parlant de la fonction inverse) :
"on peut dire que f est derivable sur R prive de 0
le danger est le suivant:
pour tout x de R prive de 0, f'(x)<0
donc f est decroissante sur R prive de 0.
Ce qui est faux ...
Moralite mieux vaut parler de derivabilite sur un intervalle."
Euh oui d'accord, mais c'est faux non, la fonction inverse est bien décroissante sur R*, Non ?
Dérivée intervalle
8 messages
- Page 1 sur 1
Salut !
Considère la fonction définie sur par
par =|x-1|) .
.
En restreignant l'ensemble des valeurs de départ de , on a :
, on a :
 est dérivable sur
est dérivable sur 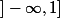 donc sur
donc sur  ;
;
 est dérivable sur
est dérivable sur 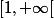 donc sur
donc sur 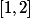 .
.
Or n'est pas dérivable en
n'est pas dérivable en  car le nombre dérivé de
car le nombre dérivé de  à gauche et à droite est différent.
à gauche et à droite est différent.
 = -1) et
et = 1) .
.
:+++:
Considère la fonction définie sur
En restreignant l'ensemble des valeurs de départ de
Or
:+++:
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
pokpak a écrit:De plus j'ai trouvé sur internet quelqu'un qui disait (en parlant de la fonction inverse) :
"on peut dire que f est derivable sur R prive de 0
le danger est le suivant:
pour tout x de R prive de 0, f'(x)<0
donc f est decroissante sur R prive de 0.
Ce qui est faux ...
Moralite mieux vaut parler de derivabilite sur un intervalle."
Euh oui d'accord, mais c'est faux non, la fonction inverse est bien décroissante sur R*, Non ?
On parle de la monotonie d'une fonction sur un intervalle, pas sur une réunion d'intervalles.
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
Le problème qui peut se poser, c'est que si tu dis que la fonction inverse est décroissante sur 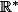 , on pourrait alors dire que, par définition d'une fonction décroissante :
, on pourrait alors dire que, par définition d'une fonction décroissante :
Si tu prends deux réels non nuls et
et  tels que
tels que  .
.
Or c'est faux ! Par exemple, si tu prends, et
et  , on a
, on a  .
.
:+++:
Si tu prends deux réels non nuls
Or c'est faux ! Par exemple, si tu prends,
:+++:
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
pokpak a écrit:Je crois saisir,
Mais la fonction inverse est décroissante sur R*, alors est-ce faux de le dire, ou est-ce vrai "officieusement" mais on ne peut pas le dire car on ne peut pas parler de monotonie sur une réunion d'intervalle ?
La fonction inverse est décroissante sur ]-inf;0[ et elle est décroissante sur ]0;+inf[ mais on ne peut pas dire qu'elle est décroissante sur R*.
En effet :
Si a et b appartiennent à ]-inf;0[ et si a 1/b
De même si a et b appartiennent à ]0;+inf[
Par contre, si a et b appartiennent à R* et si a 1/b.
En effet si a < 0 < b alors 1/a < 1/b
8 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 36 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
