Equation fonctionnelle [OIM 2015]
Olympiades mathématiques, énigmes et défis
-
ffpower
- Membre Complexe
- Messages: 2542
- Enregistré le: 13 Déc 2007, 04:25
-
 par ffpower » 14 Oct 2015, 18:35
par ffpower » 14 Oct 2015, 18:35
Donc allons y. On suppose f(0)=0, et on veut montrer que f=Id. On veut donc étudier Fix(f)={x |f(x)=x} et montrer que Fix(f)=R
Je résume les propriétés que j'ai écrites dans mon premier post.
1) Pour tout x réel,
\in Fix(f))
et
\in Fix(f))
2)
)
et
)
3)
\Rightarrow 2x \in Fix(f))
et
\Rightarrow -x \in Fix(f))
(note: mais en réalité, á part 2) je ne vais me servir de quasiment rien de tout ça :p)
Ma ligne de mire est de prouver que
\Rightarrow x+1 \in Fix(f))
.
(J'ai en effet noté un moyen simple de conclure á partir de cette implication).
Suite au prochain post, histoire d'aérer

-
ffpower
- Membre Complexe
- Messages: 2542
- Enregistré le: 13 Déc 2007, 04:25
-
 par ffpower » 14 Oct 2015, 18:51
par ffpower » 14 Oct 2015, 18:51
Je pars donc de l'équation initiale, en posant un changement de variables
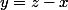
:
)+f(x(z-x))=x+f(z)+(z-x)f(x))
En particulier:
si
)
et
)
:
+f(x(z-x))=x+z+x(z-x))
En prenant x=1 puis x=-1, j'obtient en particulier les 2 équations suivantes:
Si
)
:
+f(z-1)=2z)
+f(-(z+1))=-2)
En soustrayant les deux equations:
Si
)
:
-f(-(z+1))=2(z+1)) Morale de ce post:
Morale de ce post:Si
)
,
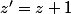
vérifie
-f(-z')=2z')
-
ffpower
- Membre Complexe
- Messages: 2542
- Enregistré le: 13 Déc 2007, 04:25
-
 par ffpower » 14 Oct 2015, 19:01
par ffpower » 14 Oct 2015, 19:01
Il existe un autre moyen de relier
)
et
)
:
Je repars de l'equation
)+f(x(z-x))=x+f(z)+(z-x)f(x))
et je fais z=0:
+f(-x^2)=x-xf(x))
En remplaçant x par -x:
+f(-x^2)=-x+xf(x))
Je soustrais ces deux dernieres équations pour éliminer le
)
et obtenir une relation entre f(x) et f(-x):
-f(-x)=2x-x(f(x)+f(-x)),)
qui peut se réécrire
f(x)+(x-1)f(-x)=2x) Morale de ce post:
Morale de ce post:Pour tout
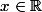
:
f(x)+(x-1)f(-x)=2x)
-
ffpower
- Membre Complexe
- Messages: 2542
- Enregistré le: 13 Déc 2007, 04:25
-
 par ffpower » 14 Oct 2015, 19:19
par ffpower » 14 Oct 2015, 19:19
Maintenant, je cumule le résultat des 2 posts précédents:
Si
)
, alors
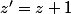
vérifie les deux équations:
-f(-z')=2z')
f(z')+(z'-1)f(-z')=2z')
La résolution de ce systeme en
)
et
)
donne
=z')
et
=-z') Conclusion de tout ça:
Conclusion de tout ça:\Rightarrow z'=z+1 \in Fix(f))
J'ai dit qu'il était facile de conclure á partir de cette implication. Voyons maintenant pourquoi:
Repartons de l'équation initiale:
)+f(xy)=x+f(x+y)+yf(x))
Faisons

)+f(y)=1+f(1+y)+y)
On sait que
\in Fix(f))
(á cause de
)=f(x))
)
Donc
\in Fix(f))
, cad
)=1+f(1+y))
Du coup, l'equation se simplifie en
+f(y)=1+f(1+y)+y)
=y)
:zen:

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 14 Oct 2015, 20:37
par chan79 » 14 Oct 2015, 20:37
ffpower a écrit:(Pour ça j ai par exemple reussi á prouver que f(n)=n pour n entier, mais ya peut etre meme plus immediat)
J'ai fait ça aussi, par récurrence. Je regarderai ton autre démo demain. :zen:

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 15 Oct 2015, 08:42
par chan79 » 15 Oct 2015, 08:42
ffpower a écrit:Morale de ce post:Si
)
,
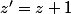
vérifie
+f(-z')=2z')
Bravo pour ta démo !!!
Un petit problème de signe ci-dessus mais qui ne remet pas en cause la suite.
Ca doit être
-f(-z')=2z')
-
ffpower
- Membre Complexe
- Messages: 2542
- Enregistré le: 13 Déc 2007, 04:25
-
 par ffpower » 15 Oct 2015, 12:05
par ffpower » 15 Oct 2015, 12:05
Merci :we:
Je rectifie de ce pas cette coquille :++:
-
ffpower
- Membre Complexe
- Messages: 2542
- Enregistré le: 13 Déc 2007, 04:25
-
 par ffpower » 15 Oct 2015, 21:14
par ffpower » 15 Oct 2015, 21:14
pour le cas f(0)=2, j ai une solution courte:
pour y=1, l equation donne, aprés simplification
f(x+f(x+1))=x+f(x+1), donc:
pour tout x, x+f(x+1) est un point fixe de f
Pour x=0, l'equation devient
f(f(y))+2=f(y)+2y
En particulier, si y est point fixe de f, ça devient
y+2=y+2y
donc y=1. Ainsi
L'unique point fixe éventuel de f est 1
Conclusion:
Pour tout x, x+f(x+1)=1
Ça donne donc f(x)=2-x

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 15 Oct 2015, 22:30
par chan79 » 15 Oct 2015, 22:30
Super :++:

-
Lostounet
- Membre Légendaire
- Messages: 9665
- Enregistré le: 16 Mai 2009, 11:00
-
 par Lostounet » 15 Oct 2015, 23:42
par Lostounet » 15 Oct 2015, 23:42
Bravo ffpower j'adore ta deuxième preuve. :id:
La première il faut que je relise.
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 12 invités
