salut
montrer que si x,y et z sont des réels positifs tels que x+y+z=1
alors 0<= xy+yz+zx - 2xyz<= 7/27
et merci
Prob d'OIM
11 messages
- Page 1 sur 1
Olympus a écrit:Si si elle est jolie aussi, elle n'a utilisé qu'une simple étude de fonction + IAG ^^
:we:
au passage je constate que tu t'interesse aux inequations, c'est bien !
apparement tu es en 1 ere S, mais je t'invite quand meme a regarder des cours sur "l'optimisation sous contrainte(s) "
c'est assez accessible a condition d'avoir des petites notions sur les matrices, les fonctions a plusieurs variables et les differentielles, mais bon tu peux tjs regarder ..
Comme x+y+z = 1 les 3 nombres ne peuvent être simultanément >1/3 , l'un est £ 1/3 ; si c'est z £ 1/3, puisque S=xy+yz+zx-2xyz=z(x+y)+xy(1-2z) et que 1/3£1-2z alors 0£ S; même raisonnement si c'est x ou y qui est £ 1/3 et donc on a toujours 0 £ S.
Montrons maintenant que S£ 7/27. Comme précédemment supposons, par exemple, que z £ 1/3 ce qui assure 1-2z >0.
xy = 0,25((x+y))2-(x-y)2) £ 0,25(x+y)2 et S £ z(x+y)+0,25(x+y)2(1-2z) = f(z)
On a f(z) = z(1-z)+0,25(1-z)2(1-2z)=0,25(-2z3+z2+1) et f '(z) = 0,5z(1-3z) montre (faire un tableau de variation) que pour tout z entre 0 et 1/3 on a f(z)£ f(1/3)=7/27 et S £ 7/27 ; même raisonnement si c'est x ou y qui est £ 1/3 et donc on a toujours S£ 7/27 .
Rem : on a S = 7/27 ssi x = y = z =1/3. En effet, si par exemple c'est z £ 1/3 , on aura S = 7/27 ssi f(z)=7/27 et S=f(z) soit ssi z =1/3 et 0,25((x+y))2-(x-y)2)=0,25(x+y)2, soit ssi z=1/3 et x=y soit ssi x=y=z=1/3 (puisque x+y+z=1).
Montrons maintenant que S£ 7/27. Comme précédemment supposons, par exemple, que z £ 1/3 ce qui assure 1-2z >0.
xy = 0,25((x+y))2-(x-y)2) £ 0,25(x+y)2 et S £ z(x+y)+0,25(x+y)2(1-2z) = f(z)
On a f(z) = z(1-z)+0,25(1-z)2(1-2z)=0,25(-2z3+z2+1) et f '(z) = 0,5z(1-3z) montre (faire un tableau de variation) que pour tout z entre 0 et 1/3 on a f(z)£ f(1/3)=7/27 et S £ 7/27 ; même raisonnement si c'est x ou y qui est £ 1/3 et donc on a toujours S£ 7/27 .
Rem : on a S = 7/27 ssi x = y = z =1/3. En effet, si par exemple c'est z £ 1/3 , on aura S = 7/27 ssi f(z)=7/27 et S=f(z) soit ssi z =1/3 et 0,25((x+y))2-(x-y)2)=0,25(x+y)2, soit ssi z=1/3 et x=y soit ssi x=y=z=1/3 (puisque x+y+z=1).
On pose 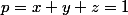 ,
, 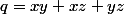 ,
, 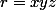
L'inégalité à démontrer se réécrit alors :
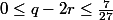
L'inégalité de Schur s'énonce comme suit :
(x-z)+y^{t}(y-x)(y-z)+z^{t}(z-x)(z-y)\geq0) pour tout réel t et réels positifs x, y,z
pour tout réel t et réels positifs x, y,z
Pour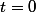 nous avons :
nous avons : (x-z)+y^0(y-x)(y-z)+z^0(z-x)(z-y)\geq0\Leftrightarrow pq-9r\geq0)
Pour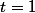 nous avons :
nous avons : (x-z)+y^{1}(y-x)(y-z)+z^{1}(z-x)(z-y)\geq0\Leftrightarrow p^{3}-4pq+9r\geq0)
De ces deux inégalités on en déduis un encadrement pour q et r :
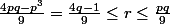 (1)
(1)
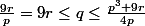 (2)
(2)
De (2) nous avons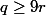 et puisque
et puisque 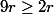 alors par transitivité,
alors par transitivité, 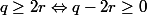
L'inégalité à démontrer se réécrit aussi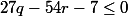
De (1) nous avons-7=3q-1)
Or il est bien connu que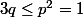 d'où
d'où 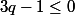 et ainsi par transitivité,
et ainsi par transitivité, 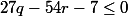
Ainsi nous avons prouvé que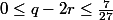
L'inégalité à démontrer se réécrit alors :
L'inégalité de Schur s'énonce comme suit :
Pour
Pour
De ces deux inégalités on en déduis un encadrement pour q et r :
De (2) nous avons
L'inégalité à démontrer se réécrit aussi
De (1) nous avons
Or il est bien connu que
Ainsi nous avons prouvé que
11 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 7 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
