Je viens de découvrir ce problème, et je me propose de regarder du côté d'éventuels points fixes.Dans ce message je me limite au cas où

est continue et
=0)
1)
Vous avez déjà vu que
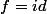
était solution, avec une infinité de points fixes donc.
2) Si
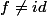
=x_0+\lambda)
, avec
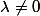
Pour tout couple
)
on a :
]+f(xy)=x+f(x+y)+yf(x))
Si je regarde au point
)
, on trouve :
]+f(0)=x_0+f(x_0))
Mais puisque
=x_0+\lambda)
et
=0)
on trouve que :
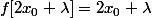
, donc un point fixe en
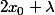
.
Je trouve ça intéressant : ca voudrait dire que dès qu'on trouve un point non fixe, alors il y a un point fixe dans les parages... Et même plusieurs en fait puisque

est continue donc on peut trouver un intervale autour de ce

tel que
 \neq x_0)
.
Bien sûr, il est possible que ce point fixe soit, toujours le même, voir éventuellement toujours 0 mais si c'est le cas, alors cela impose une relation à

, c'est à dire qu'on a forcément
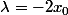
soit encore
=-x_0)
.
3)Petite remarque:
Si maintenant on suppose
=2)
, j'ai le droit d'écrire
=x_0+\lambda)
avec
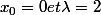
En faisant comme au 2) on a :
=2x_0+\lambda)
,
En remplacant les valurs dans l'équation on en déduit que
=0)
(ce qui est cohérent avec ce qui a déjà été trouvé)
Je me demande si on peut arriver à quelque chose par cette voie...
(to be continued...)
l'ensemble des nombres réels. Déterminer toutes les fonctions
qui vérifient l'équation
pour tous réels
et
.

