Bonjour tout le monde un coups de main svp j'ai ds demain et ca peut me venir en spe ce genre d'exercice.
Montrer par reccurence que,pour tout entier n,4^n - 1 est un multiple de 3.
Initialisation:
Pour n = 0 , U0 = 4^0 - 1 = 0 or 0 est un multiple de 3.
Heredite:
Supposons que pour tout entier k >= 0 Uk = 4^k - 1 est un multiple de 3 et montrons que
Uk+1 = 4^(k + 1) - 1 est un multiple de 3.
On a : Uk+1 = 4^(k + 1) - 1 = 4*4^k - 1 Or (4^k - 1 etant un multiple de 3 par hypothese de reccurence peut donc s'ecrire 3a.on remplace)
Uk+1 = 4*3a - 1 = 12a - 1.
Je m'arrete ici je sais plus quoi faire apres et je pense que j'ai fait une erreur de l'aide svp.
Raisonnement par reccurence - Tle S.
8 messages
- Page 1 sur 1
mathelot a écrit:
Merci de repondre Mathelot mais je ne comprend pas comment avez vous transformer
4^(n + 1) - 1 = 4(4^n+ 1) + 3.
Clarifier un peu ce que vous avez fait.
Autre chose dont je suis pas convaincu c'est que le 2eme membre si on le developpe n'equivaut pas le premier membre 4^(n + 1) - 1 # 4^(n + 1) + 7.
Je m'y perd,svp expliquer... :hein:
Combattant204 a écrit:Merci de repondre Mathelot mais je ne comprend pas comment avez vous transformer
4^(n + 1) - 1 = 4(4^n+1) + 3. <----ici, c'est faux
Clarifier un peu ce que vous avez fait.
Autre chose dont je suis pas convaincu c'est que le 2eme membre si on le developpe n'equivaut pas le premier membre 4^(n + 1) - 1 # 4^(n + 1) + 7.
Je m'y perd,svp expliquer... :hein:
.....................
On suppose donc que la formule est bonne au rang  , c'est à dire qu'il existe un entier
, c'est à dire qu'il existe un entier 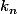 tel que
tel que

Ce qu'on veut montrer, c'est que la formule est valable au rang , c'est à dire qu'il existe un autre entier
, c'est à dire qu'il existe un autre entier 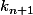 , tel que :
, tel que :

Ce qu'il faut, c'est donc s'arranger pour introduire la première formule, que l'on suppose vraie, dans la seconde...
Par exemple :

Bon, ici on a introduit le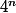 ... Essayons d'introduire le -1. Facile :
... Essayons d'introduire le -1. Facile :
 -1)
OK ?
Puisqu'on suppose que la première formule (au rang n) est vraie, on remplace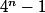 dans la dernière équation par celle-ci, d'où :
dans la dernière équation par celle-ci, d'où :
 -1 = 4*(3k_n+1)-1)
Soit :

Ce qui est vraiment top cool, c'est qu'on peut factoriser ça par 3, d'accord (*) ?
) .
.
Du coup, on l'a trouvé notre ... .
... .
Précisément, on a :
 avec
avec

Au passage on vérifie bien que les nombres ne nous font pas une farce et que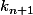 est entier, sinon le raisonnement n'est pas valable... OK, c'est bien le cas puisque si
est entier, sinon le raisonnement n'est pas valable... OK, c'est bien le cas puisque si 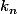 est entier, alors
est entier, alors  aussi.
aussi.
La récurrence est donc montrée(**).
(*) En fait, il ne faut ici pas perdre de vue ce que l'on cherche: nous VOULONS montrer que la formule
reste vraie au rang et nous prenons donc les dispositions pour factoriser par 3, quelque part en "priant" pour que cela fonctionne.
et nous prenons donc les dispositions pour factoriser par 3, quelque part en "priant" pour que cela fonctionne.
(**) Bien entendu, ne pas oublir de tester (vous l'avez fait) pour la valeur initiale sinon toute la démonstration s'effondre. C'est un piège classique.
Ce qu'on veut montrer, c'est que la formule est valable au rang
Ce qu'il faut, c'est donc s'arranger pour introduire la première formule, que l'on suppose vraie, dans la seconde...
Par exemple :
Bon, ici on a introduit le
OK ?
Puisqu'on suppose que la première formule (au rang n) est vraie, on remplace
Soit :
Ce qui est vraiment top cool, c'est qu'on peut factoriser ça par 3, d'accord (*) ?
Du coup, on l'a trouvé notre
Précisément, on a :
Au passage on vérifie bien que les nombres ne nous font pas une farce et que
La récurrence est donc montrée(**).
(*) En fait, il ne faut ici pas perdre de vue ce que l'on cherche: nous VOULONS montrer que la formule
reste vraie au rang
(**) Bien entendu, ne pas oublir de tester (vous l'avez fait) pour la valeur initiale sinon toute la démonstration s'effondre. C'est un piège classique.
salut
voir le post de mathafou : http://www.ilemaths.net/sujet-dm-divisibilite-ts-spe-651131.html#msg5528921
et le suivant ...
voir le post de mathafou : http://www.ilemaths.net/sujet-dm-divisibilite-ts-spe-651131.html#msg5528921
et le suivant ...
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
La démonstration d'une formule par récurrence est bien souvent élégante et concise. Lorsqu'on maîtrise la technique, cela devient presque un jeu de plage (en tout cas pour les problèmes scolaires simples).
L'inconvénient de cette technique est qu'elle suppose de connaitre la formule à l'avance...
L'étudiant aura donc intérêt à envisager ce mode de démonstration lorsque la réponse sera "soufflée", via des questions du genre "montrer que 'ceci' égale 'cela' sur les problèmes qui s'y prêtent (nombres entiers, etc.).
Pour le mathématicien "pro" (qui travaille en principe sur des problèmes inédits), c'est évidemment plus compliqué...
mais il pourra l'utiliser pour faire une démonstration élégante d'une formule par ailleurs découverte laborieusement ou pour tester rapidement ses intuitions de formules.
L'inconvénient de cette technique est qu'elle suppose de connaitre la formule à l'avance...
L'étudiant aura donc intérêt à envisager ce mode de démonstration lorsque la réponse sera "soufflée", via des questions du genre "montrer que 'ceci' égale 'cela' sur les problèmes qui s'y prêtent (nombres entiers, etc.).
Pour le mathématicien "pro" (qui travaille en principe sur des problèmes inédits), c'est évidemment plus compliqué...
mais il pourra l'utiliser pour faire une démonstration élégante d'une formule par ailleurs découverte laborieusement ou pour tester rapidement ses intuitions de formules.
8 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 64 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
