Bonjour à toutes & à tous,
J'aurais besoin d'un moyen, si possible simple, pour faire ceci :
Obtenir une fonction de la forme y=f(x) pour une courbe, mais ladite courbe étant indiquée par une autre fonction, et c'est là que cela se complique :
Cette dernière fonction indique le rayon de courbure de ladite courbe, MAIS "le long de la courbe" (et pas en fonction de x), c'est-à-dire selon un repère dont l'un des axes est tangent à la courbe "en tout point" (il la suit, si vous préférez) - ce serait là typiquement ce que l'on appelle le repère de Frenet.
Aussi, quelqu'un a-t-il svp déjà rencontré ce cas, ou alors peut-être que avez-vous quelques idées pour moi ?
Merci d'avance, cordialement,
Amka
Pour passer du repere curviligne (du style Frenet) au repere XY standard.
13 messages
- Page 1 sur 1
Salut,
C'est extrêmement "classique" comme problème sur le plan théorique, à savoir que :
Théorème :
Étant donnée une fonction régulière) (définie sur un intervalle de R), il existe, à isométrie directe prés une unique courbe
(définie sur un intervalle de R), il existe, à isométrie directe prés une unique courbe ) paramétrée par longueur d'arc telle que, quelque soit
paramétrée par longueur d'arc telle que, quelque soit  , le rayon de courbure (orienté) de la courbe au point
, le rayon de courbure (orienté) de la courbe au point ) soit
soit ) .
.
Sauf qu'il y a plusieurs problèmes :
1) Dans la pratique, pour trouver connaissant
connaissant  il faut résoudre une équation différentielle que la plupart du temps... on ne sait pas résoudre de façon exacte.
il faut résoudre une équation différentielle que la plupart du temps... on ne sait pas résoudre de façon exacte.
2) Il est complètement évident qu'en ne connaissant que la courbure, on ne va en déduire la courbe qu'à isométrie directe prés donc pour avoir une unique solution, il faut se donner un point "de départ" et une direction "de départ" (comme dans toute équa. dif. en fait)
3) Parmi toutes les courbes solutions, je ne vois pas de raison particulière qu'il y en ait ne serait ce qu'une seule qui ait le bon gout de pouvoir s'exprimer sous la forme très particulière y=f(x) (ou alors uniquement localement)
C'est extrêmement "classique" comme problème sur le plan théorique, à savoir que :
Théorème :
Étant donnée une fonction régulière
Sauf qu'il y a plusieurs problèmes :
1) Dans la pratique, pour trouver
2) Il est complètement évident qu'en ne connaissant que la courbure, on ne va en déduire la courbe qu'à isométrie directe prés donc pour avoir une unique solution, il faut se donner un point "de départ" et une direction "de départ" (comme dans toute équa. dif. en fait)
3) Parmi toutes les courbes solutions, je ne vois pas de raison particulière qu'il y en ait ne serait ce qu'une seule qui ait le bon gout de pouvoir s'exprimer sous la forme très particulière y=f(x) (ou alors uniquement localement)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Bon, on va refaire un petit bout de la théorie...
On prend une courbe paramétrée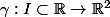 de classe
de classe  que l'on suppose parcourue par longueur d'arc, c'est à dire telle que,
que l'on suppose parcourue par longueur d'arc, c'est à dire telle que, |=1) .
.
On a donc|\gamma'(t)\rangle=1) (produit scalaire) pour tout t de I et, en dérivant on en déduit que
(produit scalaire) pour tout t de I et, en dérivant on en déduit que |\gamma''(t)\rangle=0) :
: ) et
et ) sont orthogonaux.
sont orthogonaux.
Pour tout vecteur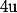 de
de 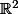 notons
notons 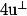 l'image de
l'image de 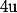 par la rotation d'angle
par la rotation d'angle 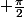 (si
(si ) dans une b.o.n.d. alors
dans une b.o.n.d. alors ) )
)
Il existe alors un (unique) réel) tel que
tel que =r(t)\gamma'(t)^\perp) qui est appellé "courbure de
qui est appellé "courbure de 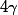 au point
au point ) " (et ce qu'on appelle le "rayon de courbure", c'est
" (et ce qu'on appelle le "rayon de courbure", c'est }) qui n'existe que lorsque
qui n'existe que lorsque \not=0) ).
).
On a aussi (autre définition possible),\gamma''(t))=\det(\gamma'(t), r(t) \gamma'(t)^\perp)=r(t)\langle \gamma'(t)|\gamma'(t)\rangle=r(t)) (déterminant calculé dans n'importe quelle base orthonormée directe)
(déterminant calculé dans n'importe quelle base orthonormée directe)
Bilan "calculatoire" : si on écrit=(x(t),y(t))) on a
on a  et, si on connait la fonction
et, si on connait la fonction 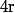 et qu'on cherche
et qu'on cherche 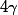 , c'est ces équations là qu'il faut résoudre.
, c'est ces équations là qu'il faut résoudre.
Après, contrairement à ce que j'avais dit (j'ai peut-être confondu avec la dimension 3 où, connaissant la courbure et la torsion, on a du mal à intégrer l'équa-diff) on peut pas mal avancer dans la résolution :
La première équation dit que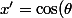) et
et 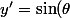) où
où 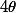 est une fonction de
est une fonction de 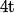 et si on injecte ça dans la deuxième équation, ça donne
et si on injecte ça dans la deuxième équation, ça donne \times\theta'\cos(\theta)-\sin(\theta)\times-\theta'\sin(\theta)=r) c'est à dire
c'est à dire 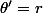 (ce qui donnait d'ailleurs une troisième possibilité simple pour la définition du rayon de courbure)
(ce qui donnait d'ailleurs une troisième possibilité simple pour la définition du rayon de courbure)
Donc il suffit de prendre pour une primitive quelconque de
une primitive quelconque de 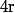 (ce qui laisse le choix de la "direction de départ" de la courbe) puis d'en déduire
(ce qui laisse le choix de la "direction de départ" de la courbe) puis d'en déduire 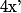 et
et 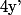 puis d'en déduire
puis d'en déduire 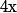 et
et 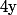 (à une constante près ce qui laisse le choix du "point de départ" de la courbe).
(à une constante près ce qui laisse le choix du "point de départ" de la courbe).
Donc c'est pas vraiment un problème de résolution d'équa. diff. mais uniquement des problèmes de calculs de primitives (qu'on risque en général de pas arriver à trouver explicitement...)
On prend une courbe paramétrée
On a donc
Pour tout vecteur
Il existe alors un (unique) réel
On a aussi (autre définition possible)
Bilan "calculatoire" : si on écrit
Après, contrairement à ce que j'avais dit (j'ai peut-être confondu avec la dimension 3 où, connaissant la courbure et la torsion, on a du mal à intégrer l'équa-diff) on peut pas mal avancer dans la résolution :
La première équation dit que
Donc il suffit de prendre pour
Donc c'est pas vraiment un problème de résolution d'équa. diff. mais uniquement des problèmes de calculs de primitives (qu'on risque en général de pas arriver à trouver explicitement...)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Ben en fait ça a l'air de parfaitement se résoudre ton truc (et ça me surprend... :doh:)
En changeant l'origine des abscisses curvilignes sur la courbe (i.e. le t=0), ainsi que le sens de parcours et en faisant une homothétie de la courbe (ce qui multiplie la courbure par une constante), on peut se ramener à=r(t)=\frac{1}{2\sqrt{t}}) donc
donc =\sqrt{t}) (à une constante près, c'est à dire à rotation de la courbe près)
(à une constante près, c'est à dire à rotation de la courbe près)
En identifiant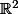 à
à 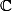 ça donne
ça donne =e^{i\sqrt{t}}) donc
donc =\int_{0}^{t}e^{i\sqrt{u}}\,du) (à une constante complexe prés, c'est à dire à translation de la courbe près)
(à une constante complexe prés, c'est à dire à translation de la courbe près)
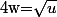 donne
donne =\int_{0}^{\sqrt{t}}e^{iw}\,2wdw\) puis une i.p.p. donne
puis une i.p.p. donne
<br />=2\Big[ \frac{e^{iw}}{i}w \Big]_{0}^{\sqrt{t}}-2\int_{0}^{\sqrt{t}}\frac{e^{iw}}{i}\,dw<br />=-2i\sqrt{t}e^{i\sqrt{t}}+2e^{i\sqrt{t}}\,(+Cst)=2(1-i\sqrt{t})e^{i\sqrt{t}})
En virant le 2 (homothétie) et en reparamétrant (donc on a plus une p.l.a.), ça donne=(1-is)e^{is}) c'est à dire
c'est à dire =\cos(s)+s\,\sin(s)\cr y(s)=\sin(s)-s\,\cos(s)}\right.)
qui est simplement... la développante du cercle trigo...
En changeant l'origine des abscisses curvilignes sur la courbe (i.e. le t=0), ainsi que le sens de parcours et en faisant une homothétie de la courbe (ce qui multiplie la courbure par une constante), on peut se ramener à
En identifiant
En virant le 2 (homothétie) et en reparamétrant (donc on a plus une p.l.a.), ça donne
qui est simplement... la développante du cercle trigo...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Super,
Ces informations me sont très précieuses et je trouve le cheminement habile.
J'ai profité de cette journée pour me rafraîchir la mémoire en ce qui concerne l'intégration par parties et la substitution, ça faisait un moment et ça fait du bien. J'ai décortiqué par ailleurs (du moins en partie) tes messages.
Ceci dit, il y a un truc qui m'intrigue : pour passer de
x' carré + y' carré = 1
vers
x' = cos(Thêta)
y' = sin(Thêta)
Quelle est donc stp la formule ? Il n'y a donc au monde rien d'autre que ce cos & sin pour satisfaire à ceci ? Dans quelle "trappe" tombe donc :
x' = sin(Thêta)
y' = cos(Thêta)
afin que la première formulation (x' = cos(Thêta) et y' = sin(Thêta)) nous soit suffisante ?
A+
Ces informations me sont très précieuses et je trouve le cheminement habile.
J'ai profité de cette journée pour me rafraîchir la mémoire en ce qui concerne l'intégration par parties et la substitution, ça faisait un moment et ça fait du bien. J'ai décortiqué par ailleurs (du moins en partie) tes messages.
Ceci dit, il y a un truc qui m'intrigue : pour passer de
x' carré + y' carré = 1
vers
x' = cos(Thêta)
y' = sin(Thêta)
Quelle est donc stp la formule ? Il n'y a donc au monde rien d'autre que ce cos & sin pour satisfaire à ceci ? Dans quelle "trappe" tombe donc :
x' = sin(Thêta)
y' = cos(Thêta)
afin que la première formulation (x' = cos(Thêta) et y' = sin(Thêta)) nous soit suffisante ?
A+
Dire que deux réels x et y fixés vérifient x²+y²=1, ça veut exactement dire (via Pythagore) que le point M:(x,y) est située à une distance 1 de l'origine O:(0,0), c'est à dire qu'il est sur le "cercle trigo." (cercle de centre O et de rayon 1).
Et comme, quasi par définition (encore que ça dépend de la définition qu'on prend...) les points du cercle trigo. sont aussi très exactement ceux de coordonnées (cos(theta),sin(theta)), ça te dit qu'il existe theta (unique modulo 2pi) tel que x=cos(theta) et y=sin(theta).
C'est une espèce de "réciproque" du résultat archi. connu disant que cos²+sin²=1.
Après, lorsque x et y sont des réels "variables", c'est à dire des fonctions d'un certain t, c'est un peu plus technique de montrer que l'on peut trouver une fonction t->theta(t) telle que, pour tout t, on ait x(t)=cos(theta(t)) et y(t)=sin(theta(t)) et telle que la fonction t->théta(t) soit "aussi régulière" que les fonction t->x(t) et t->y(t) [i.e. continue, dérivable, de classe C1, etc..] mais je trouve que c'est extrêmement intuitif (la difficulté réside évidement dans le fait que au départ, pour tout t, theta(t) n'est unique que modulo 2pi)
Ici, pour que tout marche "sans soucis", il faut supposer gamma de classe C2 au début pour obtenir que r est continue et, réciproquement, partant de r continue, tu construit une courbe gamma (unique à isométrie près) qui st de classe C2.
Et comme, quasi par définition (encore que ça dépend de la définition qu'on prend...) les points du cercle trigo. sont aussi très exactement ceux de coordonnées (cos(theta),sin(theta)), ça te dit qu'il existe theta (unique modulo 2pi) tel que x=cos(theta) et y=sin(theta).
C'est une espèce de "réciproque" du résultat archi. connu disant que cos²+sin²=1.
Après, lorsque x et y sont des réels "variables", c'est à dire des fonctions d'un certain t, c'est un peu plus technique de montrer que l'on peut trouver une fonction t->theta(t) telle que, pour tout t, on ait x(t)=cos(theta(t)) et y(t)=sin(theta(t)) et telle que la fonction t->théta(t) soit "aussi régulière" que les fonction t->x(t) et t->y(t) [i.e. continue, dérivable, de classe C1, etc..] mais je trouve que c'est extrêmement intuitif (la difficulté réside évidement dans le fait que au départ, pour tout t, theta(t) n'est unique que modulo 2pi)
Ici, pour que tout marche "sans soucis", il faut supposer gamma de classe C2 au début pour obtenir que r est continue et, réciproquement, partant de r continue, tu construit une courbe gamma (unique à isométrie près) qui st de classe C2.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Très bien, j'y vois plus clair merci bien.
Ceci dit, quand je rapporte ta réponse à mon équation de départ disons R(p) = A racine(L-p), j'obtiens
x(p) = ( cos(q) + q sin(q) ) / (2 A carré)
y(p) = ( sin(q) - q cos(q) ) / (2 A carré)
avec q = 2 A racine( L - p )
Il faudra d'ailleurs que je potasse encore un peu tout ça, je crois qu'il y a un ou deux autres points que je n'ai toujours pas bien compris.
:-)
Ceci dit, quand je rapporte ta réponse à mon équation de départ disons R(p) = A racine(L-p), j'obtiens
x(p) = ( cos(q) + q sin(q) ) / (2 A carré)
y(p) = ( sin(q) - q cos(q) ) / (2 A carré)
avec q = 2 A racine( L - p )
Il faudra d'ailleurs que je potasse encore un peu tout ça, je crois qu'il y a un ou deux autres points que je n'ai toujours pas bien compris.
:-)
C'est (sans doute) un truc de ce style là.
De toute façon, c'est une des développante d'un certain cercle et j'ai pas regardé quel devait être le rayon du cercle ni quel origine on devait prendre sur le cercle pour que ça donne "pile poil" tes équations de départ.
De toute façon, il faut bien voir que les équations que tu donne là ne sont qu'UNE des multiples solutions au problème (rappel : la courbe "solution" n'est connue qu'à isométrie directe prés)
De toute façon, c'est une des développante d'un certain cercle et j'ai pas regardé quel devait être le rayon du cercle ni quel origine on devait prendre sur le cercle pour que ça donne "pile poil" tes équations de départ.
De toute façon, il faut bien voir que les équations que tu donne là ne sont qu'UNE des multiples solutions au problème (rappel : la courbe "solution" n'est connue qu'à isométrie directe prés)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
a) Je sais pas du tout s'il a "un nom" (à mon avis non, mais comme je connais le nom de quasiment aucun théorème, c'est pas vraiment une preuve...)
b) En plus, la preuve complète, tu l'a dans la fin du post. qui suit en... 3 lignes... : c'est pas trop compliqué... :dodo:
b) En plus, la preuve complète, tu l'a dans la fin du post. qui suit en... 3 lignes... : c'est pas trop compliqué... :dodo:
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
13 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 9 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
