bonjour,
voici un énoncé d'exercice :
d:y=( -5/3)x - 7/3 et d': y =(1/5)x+7/5 sont deux droites dans un repère
a) justifier que d et d' sont sécantes
b) on a utilisé le calcul formel geogebra pour trouver les coordonnées du point d'intersection des droites d et d'
vérifier le résultat affiché
calcul formel
résoudre [(y=(-5/3)x-7/3 , y=(1/5x+7/5 , x,y)]
-->(x=-2 y=1)
pouvez vous m'aider svp
Droites
13 messages
- Page 1 sur 1
danyboone59 a écrit:bonjour,
voici un énoncé d'exercice :
d:y=( -5/3)x - 7/3 et d': y =(1/5)x+7/5 sont deux droites dans un repère
a) justifier que d et d' sont sécantes
b) on a utilisé le calcul formel geogebra pour trouver les coordonnées du point d'intersection des droites d et d'
vérifier le résultat affiché
calcul formel
résoudre [(y=(-5/3)x-7/3 , y=(1/5x+7/5 , x,y)]
-->(x=-2 y=1)
pouvez vous m'aider svp
Deux droites sont sécantes si elles ne sont pas parallèles ou confondues, qu'est ce qui montre que deux droites exprimées sous forme d'equation ne sont pas parallèles ?
Bonjour,
L' équation (réduite) d'une droite est de la forme =ax+b (si elles ne sont pas "verticales", dans ce cas c'est x = constante) où :
* a est le coefficient directeur de la droite
* b l'ordonnée à l'origine
Quelles définitions pour ces deux notions ?
Lorsque tu auras rafraîchi ta mémoire, tu seras en mesure de répondre au a)
Bien entendu, tu pourrais résoudre le système :

mais c'est ce que fait geogebdra dans le b), donc il ne faut pas anticiper...
Bye
PS : je suis décidément toujours trop bavard...
je pense qu'il faut résoudre les équations?
L' équation (réduite) d'une droite est de la forme =ax+b (si elles ne sont pas "verticales", dans ce cas c'est x = constante) où :
* a est le coefficient directeur de la droite
* b l'ordonnée à l'origine
Quelles définitions pour ces deux notions ?
Lorsque tu auras rafraîchi ta mémoire, tu seras en mesure de répondre au a)
Bien entendu, tu pourrais résoudre le système :
mais c'est ce que fait geogebdra dans le b), donc il ne faut pas anticiper...
Bye
PS : je suis décidément toujours trop bavard...
takezo a écrit:Bonjour,
L' équation (réduite) d'une droite est de la forme =ax+b (si elles ne sont pas "verticales", dans ce cas c'est x = constante) où :
* a est le coefficient directeur de la droite
* b l'ordonnée à l'origine
Quelles définitions pour ces deux notions ?
Lorsque tu auras rafraîchi ta mémoire, tu seras en mesure de répondre au a)
Bien entendu, tu pourrais résoudre le système :
mais c'est ce que fait geogebdra dans le b), donc il ne faut pas anticiper...
Bye
PS : je suis décidément toujours trop bavard...
oui ok les deux coefficients directeurs étant différents donc les deux droites sont sécantes...
par contre je n'arrive pas à résoudre le système :
y= (-5/)x -7/3
y= (1/5)x+7/5
pouvez vous m'aider svp
si je demande de l'aide c'est que je suis en difficulté en maths
merci
Bon là, je présume que tu es gêné par les dénominateurs...
Écrit comme ça, ce système revient à résoudre :

Le dénominateur commun est 15 :

On multiplie alors les deux membres par 15 et il vient :
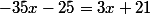
que tu dois résoudre pour trouver x..
MAIS
l'énoncé dit :
vérifier le résultat affiché
il ne te demande pas de résoudre le système !
Geogebra l'a fait.
Donc tu va vérifier que le point de coordonnées (-2;1) est bien sur les deux droites, donc que c'est bien leur point d'intersection.
Pour ça, tu vas montrer que les coordonnées de ce point vérifient l'équation de chaque droite
PS : Veux-tu vérifier tes équations de droite ? Ça ne colle pas...
(-2:1) n'est pas sur la droite d'équation
Écrit comme ça, ce système revient à résoudre :
Le dénominateur commun est 15 :
On multiplie alors les deux membres par 15 et il vient :
que tu dois résoudre pour trouver x..
MAIS
l'énoncé dit :
vérifier le résultat affiché
il ne te demande pas de résoudre le système !
Geogebra l'a fait.
Donc tu va vérifier que le point de coordonnées (-2;1) est bien sur les deux droites, donc que c'est bien leur point d'intersection.
Pour ça, tu vas montrer que les coordonnées de ce point vérifient l'équation de chaque droite
PS : Veux-tu vérifier tes équations de droite ? Ça ne colle pas...
(-2:1) n'est pas sur la droite d'équation
Bon là, je présume que tu es gêné par les dénominateurs...
Écrit comme ça, ce système revient à résoudre :

Le dénominateur commun est 15 :

On multiplie alors les deux membres par 15 et il vient :
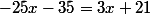
que tu dois résoudre pour trouver x..
MAIS
l'énoncé dit :
vérifier le résultat affiché
il ne te demande pas de résoudre le système !
Geogebra l'a fait.
Donc tu va vérifier que le point de coordonnées (-2;1) est bien sur les deux droites, donc que c'est bien leur point d'intersection.
Pour ça, tu vas montrer que les coordonnées de ce point vérifient l'équation de chaque droite
Écrit comme ça, ce système revient à résoudre :
Le dénominateur commun est 15 :
On multiplie alors les deux membres par 15 et il vient :
que tu dois résoudre pour trouver x..
MAIS
l'énoncé dit :
vérifier le résultat affiché
il ne te demande pas de résoudre le système !
Geogebra l'a fait.
Donc tu va vérifier que le point de coordonnées (-2;1) est bien sur les deux droites, donc que c'est bien leur point d'intersection.
Pour ça, tu vas montrer que les coordonnées de ce point vérifient l'équation de chaque droite
takezo a écrit:Bon là, je présume que tu es gêné par les dénominateurs...
Écrit comme ça, ce système revient à résoudre :
Le dénominateur commun est 15 :
On multiplie alors les deux membres par 15 et il vient :
que tu dois résoudre pour trouver x..
MAIS
l'énoncé dit :
vérifier le résultat affiché
il ne te demande pas de résoudre le système !
Geogebra l'a fait.
Donc tu va vérifier que le point de coordonnées (-2;1) est bien sur les deux droites, donc que c'est bien leur point d'intersection.
Pour ça, tu vas montrer que les coordonnées de ce point vérifient l'équation de chaque droite
Ah ok je dois vérifier le résultat comme ceci :
y = (-5/3)-2-7/3
y=10/3-7/3
y=3/3
y=1
y=1/5(-2)+7/5
y=(-2/5)+7/5=5/5=1
c'est bien ça?
merci
danyboone59 a écrit:Ah ok je dois vérifier le résultat comme ceci :
y = (-5/3)-2-7/3
y=10/3-7/3
y=3/3
y=1
y=1/5(-2)+7/5
y=(-2/5)+7/5=5/5=1
c'est bien ça?
merci
Oui, rien d'autre à faire : Geogebra te donne un résultat et tu contrôles que c'est bien exact : c'est le sens du verbe vérifier...
Tu vois que ton niveau n'est pas si faible que tu veux bien le dire ! :we:
danyboone59 a écrit:pouvez vous m'aider svp
si je demande de l'aide c'est que je suis en difficulté en maths
voilà un système qui ressemble au tien , j'en ai écrit le corrigé pour que tu t'en inspires....
on multiplie les deux membres par 33
on ajoute 77x aux deux côtés de l'égalité
on soustraie 9 aux deux côtés de l'égalité
on divise les deux côtés par 71
l'égalité étant symétrique
normalement, on conserve une autre égalité pour le calcul de y
13 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 79 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
