Résolu
11 messages
- Page 1 sur 1
Bonsoir ! On ne te demande pas de calculer P et D, juste de prouver qu'ils existent, autrement dit de prouver que F est diagonalisable. Tu dois trouver une base de vecteurs propres. Donc commence par la valeur propre 1 et vois ce que ça donne : F(u) = 1.u ssi {2x + 2y = x ; x+ 3y = y} et ainsi de suite.
Je viens de faire les calculs, c'est en effet diagonalisable. L'espace propre de 1 est engendré par le vecteur (-2 ; 1) et l'espace propre de 4 est engendré par le vecteur (1 ; 1). La matrice de passage est celle qui contient ces deux vecteurs comme colonnes. Je n'ai pas détaillé pour te laisser le plaisir de tout retrouver...
Je viens de faire les calculs, c'est en effet diagonalisable. L'espace propre de 1 est engendré par le vecteur (-2 ; 1) et l'espace propre de 4 est engendré par le vecteur (1 ; 1). La matrice de passage est celle qui contient ces deux vecteurs comme colonnes. Je n'ai pas détaillé pour te laisser le plaisir de tout retrouver...
Je ne suis pas vraiment d'accord... On demande de diagonaliser, pas de montrer que c'est diagonalisable !
Tu as trouvé les valeurs propres (racines du polynome charactéristique) qui sont les éléments de la matrice diagonale D. Maintenant il te faut les vecteurs propre pour avoir la matrice de passage P.
Que vérifie un vecteur propre (x,y) associé à la valeur propre 1 ? Trouve une solution à cette équation...
Idem pour la valeur propre 4
Tu as trouvé les valeurs propres (racines du polynome charactéristique) qui sont les éléments de la matrice diagonale D. Maintenant il te faut les vecteurs propre pour avoir la matrice de passage P.
Que vérifie un vecteur propre (x,y) associé à la valeur propre 1 ? Trouve une solution à cette équation...
Idem pour la valeur propre 4
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
Tu as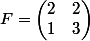 , donc
, donc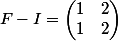 , et
, et 

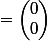
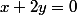 , droite vectorielle dirigée par
, droite vectorielle dirigée par .
.
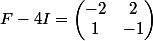 et
et 

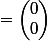
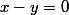 , nouvelle droite vectorielle dirigée par
, nouvelle droite vectorielle dirigée par  .
.
La matrice de passage obtenue sera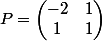 et
et
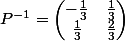
je résume; on a cherché les vecteurs tels que
tels que=1*u F-1*I=0) et on a trouvé un sous espace vectoriel qui est la droite vectorielle d'équation
et on a trouvé un sous espace vectoriel qui est la droite vectorielle d'équation 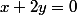 avec comme vecteur simple
avec comme vecteur simple 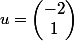 ; tu peux vérifier que
; tu peux vérifier que 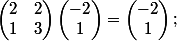
On a fait la même chose avec la valeur propre 4 et on a cherché les vecteurs tels que
tels que =4*u F-4*I=0) et on a trouvé un sous espace vectoriel qui est la droite vectorielle d'équation
et on a trouvé un sous espace vectoriel qui est la droite vectorielle d'équation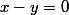 avec comme vecteur simple
avec comme vecteur simple 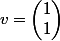 ;tu peux vérifier que
;tu peux vérifier que 
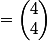 ;
;
 et
et  sont forcément linéairement indépendants et
sont forcément linéairement indépendants et ) constitue une base et dans cette base la matrice de
constitue une base et dans cette base la matrice de  a pour colonnes
a pour colonnes =u) et
et =4v) ; c'est donc la matrice
; c'est donc la matrice  quand à la matrice
quand à la matrice  dont les colonnes sont les coordonnées de
dont les colonnes sont les coordonnées de et
et  elle calcule les coordonnées de la base
elle calcule les coordonnées de la base) dans la base
dans la base ) et
et 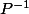 fait le contraire;
fait le contraire;
donc soit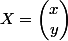 dans la base
dans la base ) ;
; 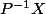 sont les coordonnées de
sont les coordonnées de  dans (
dans (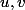) ;
; ) calcule
calcule ) dans la base
dans la base ) et enfin
et enfin ) donne
donne ) dans la base
dans la base ) et tu as donc:
et tu as donc:
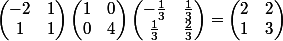
La matrice de passage obtenue sera
je résume; on a cherché les vecteurs
On a fait la même chose avec la valeur propre 4 et on a cherché les vecteurs
donc soit
La demande initiale était « je dois maintenant prouver que A = PD(P^-1) » donc si on s'en tient à cette phrase, Sylvainc2 a raison. Mais dans mon premier message j'ai quand même indiqué la méthode pour trouver la matrice de passage (en particulier j'avais donné des vecteurs propres, sans donner le détail du calcul puisqu'on n'est pas là pour tout faire à la place). Comme Youssef.eddajibi disait n'avoir rien compris, ça se trouve il n'a pas encore vu la totalité du cours sur les espaces propres et peut-être bien qu'en effet on lui demandait juste de vérifier que la matrice de départ est diagonalisable, ce serait assez logique. (Je me demande si vous avez lu toute la discussion.)
11 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 66 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
