Intégrale de ln(1+sinx) (RESOLU)

[Flovirus]

Bonjour,
Tout d'abord merci aux personnes qui prendront de leurs temps pour essayer de résoudre mon petit problème.

Je suis sur un exercice d'équation différentielle, et je bloque sur une intégrale.
Voici mon intégrale de base :

Intégrale (-xcos(x) / (1 + sin (x)))dx
Je fais par intégration par partie et j'obtiens : [-xln (1+sinx)] + intégrale (ln(1+sinx))

Et c'est là, la vraie question. J'ai ecrit que : ln(u) = uln u - u
Donc ln(1+sinx) = (1+sinx)*ln(1+sinx)-(1+sinx)

Je reste perplexe sur ce résultat, car sur certain forum, il prenne u = 1+sin x et ils font un changement de variable avec ça. Et du coup : du/dx = 1/cos x donc dx = du / cos x. Et c'est une autre paire de manche.

J'espere que je me suis fais comprendre, c'est vraiment pas facile de faire des maths sur un ordinateur.

Merci d'avance !

Flo

[Black Jack]

Tu ne vas pas t'en tirer sans fonctions spéciales.

Mais, si cela provient d'un exercice d'école, il y a une bonne probabilité que tu te sois planté dans les calculs qui précèdent.

Quel est l'énoncé initial ?

:zen:

[Flovirus]

Tu ne vas pas t'en tirer sans fonctions spéciales.

Mais, si cela provient d'un exercice d'école, il y a une bonne probabilité que tu te sois planté dans les calculs qui précèdent.

Quel est l'énoncé initial ?

:zen:

Waoou ! Merci pour cette rapide réponse, j'apprécie !

Alors pour l'exercice, voilà l'énoncé principal : Résoudre l'équation différentielle :
(1+sin(x))y'(x) - y(x)cos(x) = (1+sin(x))^3

Je suis presque sur d'avoir juste jusque là (oui l'exercice fais 2 page à résoudre xD). On est a deux dessus avec un ami.
Mon ami pense que : la dérivée de : (1+sinx)*ln(1+sinx)-(1+sinx) est = ln(1+sinx)

Et il a pas tord non ? Si nous dérivons cette équation ci dessus nous obtenous : ln(1+sinx) ??


Sinon nous pouvons décortiquer tout l'exercice ensemble ça ne me pose aucun problème. Peut être avons-nous fais une erreur ^^

Merci encore pour ton aide hein !

[Robic]

J'ai ecrit que : ln(u) = uln u - u

Je suppose que tu voulais dire :
--> primitive de ln(u) = u ln(u) - u

C'est vrai si u est la variable (notée x en général), mais pas si u est une fonction. Dans ce cas la formule est :
--> primitive de u' ln(u) = u ln(u) - u

(Il suffit de dériver u ln(u) - u pour s'en convaincre.)

---------------------
Pour l'équation différentielle, je trouve pour l'équation homogène :
,
où x ne doit pas être égal à (mettons qu'on étudie ça sur ),
d'où .

Ah, c'est dans la variation de la constante qu'apparaît la primitive de ln(1+sin x) ? Je vais voir ça...

Ah y est ! C'est plus simple que ce que tu trouves, et je soupçonne que ce que j'ai fait est juste...

Quand je « fais varier » ma constante , j'obtiens (toujours pour x dans , donc avec 1+sin x différent de 0) :
,
donc :
,
ce qui donne finalement comme solution :


(La deuxième écriture permet d'exhiber une solution particulière à gauche et la solution homogène à droite.)

Vérifions :


Donc :



Faisons la différence :
vu que les autres termes s'annulent.

Ça marche ! (Quand on a trouvé une solution d'équation différentielle, je recommande de la vérifier ensuite.)

[Flovirus]

Je suppose que tu voulais dire :
--> primitive de ln(u) = u ln(u) - u

C'est vrai si u est la variable (notée x en général), mais pas si u est une fonction. Dans ce cas la formule est :
--> primitive de u' ln(u) = u ln(u) - u

(Il suffit de dériver u ln(u) - u pour s'en convaincre.)

Merci Robic pour ta réponse !

C'est très interessant ce que tu dis là. Effectivement je confond fonction et variable.
Donc tu dis (arrête moi si je me trompe), que si on prend u(x) = sin(x) + 1 comme fonction on peut dire alors : ln u = u ln (u) - u ?

Tout dépend comment on voit la chose c'est cela ?

Merci pour ton aide enfaite
PS = quand tu dis : "primitive de u' ln(u) = u ln(u) - u" tu voulais dire : "primitive de ln(u) = u ln(u) - u"

[WillyCagnes]

attention!
ln(u) n'est pas égale à u.ln(u) -u

[Robic]

Non justement !!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!

"primitive de ln(u) = u ln(u) - u" --> FAUX ! ZÉRO ! AU COIN AVEC UN BONNET D'ÁNE !

(Désolé de crier :lol3: , mais tu me fais peur car mon intervention avait pour but uniquement de rectifier ça...)

La bonne phrase est :

"primitive de u' ln(u) = u ln(u) - u"

Pour le vérifier, dérive u ln(u) - u, tu verras.

(Note que je suis en train de compléter mon premier message en faisant la résolution de l'exercice. Pour l'instant je n'ai pas rencontré la primitive que tu indiques.)

[Flovirus]

Je suppose que tu voulais dire :
--> primitive de ln(u) = u ln(u) - u

C'est vrai si u est la variable (notée x en général), mais pas si u est une fonction. Dans ce cas la formule est :
--> primitive de u' ln(u) = u ln(u) - u

(Il suffit de dériver u ln(u) - u pour s'en convaincre.)

Pour l'équation différentielle, je trouve pour l'équation homogène :
,
d'où

Ah, c'est dans la variation de la constante qu'apparaît la primitive de ln(1+sin x) ? Je vais voir ça...

Tout à fait ! C'est dans la variation de la constante qu'apparait le petit ln
Attention l'exercice est long et calculatoire

Et sinon pour l'équation homogène Yh, moi j'ai : Kexp(-xcos(x)/1+sinx)

C'est tout bêtement la formule : Kexp(-bx/a) (x dans ce cas)

[Flovirus]

Je suppose que tu voulais dire :
--> primitive de ln(u) = u ln(u) - u

C'est vrai si u est la variable (notée x en général), mais pas si u est une fonction. Dans ce cas la formule est :
--> primitive de u' ln(u) = u ln(u) - u

(Il suffit de dériver u ln(u) - u pour s'en convaincre.)

Pour l'équation différentielle, je trouve pour l'équation homogène :
,
où x ne doit pas être égal à (mettons qu'on étudie ça sur ),
d'où .

Ah, c'est dans la variation de la constante qu'apparaît la primitive de ln(1+sin x) ? Je vais voir ça...

Ah y est ! C'est plus simple que ce que tu trouves, et je soupçonne que ce que j'ai fait est juste...

Quand je « fais varier » ma constante , j'obtiens (toujours pour x dans , donc avec 1+sin x différent de 0) :
,
donc :
,
ce qui donne finalement comme solution :


(La deuxième écriture permet d'exhiber une solution particulière à gauche et la solution homogène à droite.)

Mais je ne comprend pas. Je n'ai pas du tout cette equation homogène moi. J'ai un exponentielle moi.
Tu est d'accord avec moi que : ay(x)+by'(x) = 0
La solution homogène associé est :
Kexp(-bx/a)

[Robic]

Tu est d'accord avec moi que : ay(x)+by'(x) = 0

Non, ça c'est lorsque les coefficients a et b sont constants. Si a et b sont des fonctions, c'est plus compliqué. Revois le cours ! (Attention au bonnet d'âne... :lol3: )

Attention l'exercice est long et calculatoire

Alors, j'ai une bonne nouvelle à t'annoncer : pas du tout ! :zen: Il faut juste que tu emploies la bonne méthode...

[Flovirus]

Non, ça c'est lorsque les coefficients a et b sont constants. Si a et b sont des fonctions, il faut primitiver a/b. Revois le cours ! (Attention au bonnet d'âne... :lol3: )

La vache... La tu m'as recalé d'une force... Respect. Frenchement j'aurais galéré pendant des jours...
Je ne savais pas pour la régle des coefficients constants.. On l'a pas vu dans notre cour c'est intéressant...

Merci encore !

[Robic]

C'est étonnant ce que tu dis. Normalement on commence par voir la résolution avec coefficient constant, et ensuite avec des coefficients généraux (fonctions). J'espère que tu as une méthode pour le cas général.

Normalement, on donne aux étudiants une formule. Comme je n'ai pas de mémoire, je ne retiens jamais les formules donc je procède ainsi :

a(x)y'(x) + b(x)y(x) = 0
a(x)y'(x) = -b(x)y(x)

Pour x dans un intervalle où a et y sont non nuls (y est donc de signe constant), ça devient :
y'(x) / y(x) = -b(x) / a(x)

Puis on primitive :
ln|y(x)| = primitive de [ -b(x) / a(x) ] à une constante près

Pour obtenir y(x), il faut ensuite passer à l'exponentielle.

[Flovirus]

C'est étonnant ce que tu dis. Normalement on commence par voir la résolution avec coefficient constant, et ensuite avec des coefficients généraux (fonctions). J'espère que tu as une méthode pour le cas général.

Normalement, on donne aux étudiants une formule. Comme je n'ai pas de mémoire, je ne retiens jamais les formules donc je procède ainsi :

a(x)y'(x) + b(x)y(x) = 0
a(x)y'(x) = -b(x)y(x)

Pour x dans un intervalle où a et y sont non nuls (y est donc de signe constant), ça devient :
y'(x) / y(x) = -b(x) / a(x)

Puis on primitive :
ln|y(x)| = primitive de [ -b(x) / a(x) ] à une constante près

Pour obtenir y(x), il faut ensuite passer à l'exponentielle.

A si vu comme ça on la peut être vu..... Ok je sais ... -----> j'ai déjà le bonnet d'âne sur la tête :triste:

[Robic]

Bon, ben je pense que tu vas trouver, les calculs ne sont pas très compliqués.

Pense bien à préciser que tu te places dans ]-Pi ; Pi[ pour avoir 1+sin x non nul (donc strictement positif) et parce qu'on intègre, donc on ne définit la solution que sur une intervalle (pas sur un ensemble d'intervalle comme le serait IR privé des Pi + 2k Pi).

[Flovirus]

Bon, ben je pense que tu vas trouver, les calculs ne sont pas très compliqués.

Pense bien à préciser que tu te places dans ]-Pi ; Pi[ pour avoir 1+sin x non nul (donc strictement positif) et parce qu'on intègre, donc on ne définit la solution que sur une intervalle (pas sur un ensemble d'intervalle comme le serait IR privé des Pi + 2k Pi).

Super ! Merci pour tout frenchement avoir pris de ton temps (facile 30 min minimum) c'est très sympas!

[Robic]

De rien ! (Pour les 30 minutes, en fait je faisais autre chose en même temps...)

[deltab]

Bonsoir.

Attention à l'intervalle s'annule en. ne s'annule pas dans

[Robic]

Argh tu as raison ! Je suis allé trop vite sur ce point...

[Black Jack]

(1+sin(x))y'(x) - y(x)cos(x) = (1+sin(x))^3

Poser y = uv

y' = uv' + u'v

(1+sin(x))(uv' + u'v) - uv.cos(x) = (1 + sin(x))³

u(v'(1+sin(x)) - v.cos(x)) + u'.v.(1+sin(x))= (1 + sin(x))³

Cherchons une expression de v telle que v'(1+sin(x)) - v.cos(x)) = 0

v'/v = cos(x)/(1+sin(x))
ln|v| = ln(1+sin(x))
v = (1+sin(x))

L'équation différentielle devient alors : u'*(1+sin(x))² = (1 + sin(x))³

u' = (1 + sin(x))

u = x - cos(x) + K

Et donc y = (x - cos(x) + K) * (1 + sin(x))

Avec K une constante réelle.

:zen:

[Trident]

Pour la formule, c'est la formule de Duhamel que j'utilise personnellement car j'ai réussi à la retenir et ça gagne du temps et ça diminue le risque d'erreur par rapport à la variation de la constante !

Dans le cadre générale d'une équation de premier ordre de la forme :

où sont supposées continues, la forme générale des solutions sur un intervalle où la fonction a_1 ne s'annule pas est :



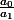où est une primitive de et K une constante réelle et un réel quelconque tel que diffère de 0.

Donc ici c'est rapide (la notation qui suit ne sera pas rigoureuse, en particulier, une fonction ne sera pas notée x -> f(x)=... )

Pour le A, il faut trouver une primitive de qui est facilement -.

Puis l'intégrale qui semble horrible ne l'est pas car elle vaut (en fait c'est une recherche de primitive, pas un vrai calcul d'intégrale)

qui vaut clairement .