Calculer primitives d'une fonction
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
elemarre
- Membre Naturel
- Messages: 39
- Enregistré le: 30 Déc 2014, 14:35
-
 par elemarre » 30 Déc 2014, 14:40
par elemarre » 30 Déc 2014, 14:40
Bonjour, je suis en première année de prépa et je bloque sur les primitives à trouver de la fonction f(u)= u^2/(1+u^2)
Je ne vois pas quelle méthode dois-je utiliser
Merci de votre aide
Elise

-
WillyCagnes
- Membre Transcendant
- Messages: 3753
- Enregistré le: 21 Sep 2013, 19:58
-
 par WillyCagnes » 30 Déc 2014, 14:45
par WillyCagnes » 30 Déc 2014, 14:45
bjr
tu ajoutes +1 et -1 au numerateur
(1+u² -1)/(1+u²)=1 - 1/(1+u²)
intégration donne I=U -arctan(u) +Cte
-
elemarre
- Membre Naturel
- Messages: 39
- Enregistré le: 30 Déc 2014, 14:35
-
 par elemarre » 30 Déc 2014, 14:52
par elemarre » 30 Déc 2014, 14:52
Merci, juste pourquoi la division (1+u^2) devient-elle une mutliplication après avoir ajouter -1 et 1 au numérateur?

-
Sake
- Habitué(e)
- Messages: 1392
- Enregistré le: 17 Juil 2014, 21:32
-
 par Sake » 30 Déc 2014, 15:30
par Sake » 30 Déc 2014, 15:30
elemarre a écrit:Merci, juste pourquoi la division (1+u^2) devient-elle une mutliplication après avoir ajouter -1 et 1 au numérateur?
Je ne vois pas de multiplication.
 - 1}{1+u^2} = 1 - \frac{1}{1+u^2})
-
elemarre
- Membre Naturel
- Messages: 39
- Enregistré le: 30 Déc 2014, 14:35
-
 par elemarre » 30 Déc 2014, 15:32
par elemarre » 30 Déc 2014, 15:32
C'était pour ça: (1+u² -1)(1+u²)
Mais finalement j'ai compris, merci beaucoup!

-
WillyCagnes
- Membre Transcendant
- Messages: 3753
- Enregistré le: 21 Sep 2013, 19:58
-
 par WillyCagnes » 30 Déc 2014, 15:48
par WillyCagnes » 30 Déc 2014, 15:48
elemarre a écrit:C'était pour ça: (1+u² -1)(1+u²)
Mais finalement j'ai compris, merci beaucoup!
sorry j'avais oublié le signe division :mur:
(1+u² -1)/(1+u²)
-
zabata29
- Messages: 5
- Enregistré le: 02 Jan 2015, 22:44
-
 par zabata29 » 02 Jan 2015, 23:02
par zabata29 » 02 Jan 2015, 23:02
bonsoir,
je bloque sur une primitive...
PRIM((x^2)/((x^4)+(x^2)+1))dx
merci pour vos réponse

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 03 Jan 2015, 02:18
par Ben314 » 03 Jan 2015, 02:18
Salut,
Il y a peut-être une astuce, mais la méthode classique marche très bien ici. C'est juste un peu long...
Il faut décomposer la fraction rationnelle en éléments simple et donc commencer par factoriser le dénominateur :
^2=\frac{1-\big(x^2\big)^3}{1-x^2}=\frac{(1-x^3)(1+x^3)}{(1-x)(1+x)}=(1+x+x^2)(1-x+x^2))
On sait alors que
)
Les deux premiers termes de la parenthèse s'intègrent en
+Cst\)
les deux suivant avec de l'arctangente une fois les dénominateurs mis sous forme canonique :
^2+\frac{3}{4}}<br />=\frac{\frac{4}{3}}{\big(\frac{2x\pm 1}{\sqrt{3}}\big)^2+1}<br />=\frac{2}{\sqrt{3}}\times\frac{\frac{2}{\sqrt{3}}}{\big(\frac{2x\pm 1}{\sqrt{3}}\big)^2+1})
qui s'intègre en
+Cst\)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
zabata29
- Messages: 5
- Enregistré le: 02 Jan 2015, 22:44
-
 par zabata29 » 03 Jan 2015, 09:56
par zabata29 » 03 Jan 2015, 09:56
Merci pour la reponse super rapide

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 03 Jan 2015, 12:30
par zygomatique » 03 Jan 2015, 12:30
salut
pour factoriser plus simplement le dénominateur ....
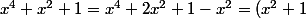^2 - x^2 = ....)
:lol3:
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
zabata29
- Messages: 5
- Enregistré le: 02 Jan 2015, 22:44
-
 par zabata29 » 03 Jan 2015, 12:47
par zabata29 » 03 Jan 2015, 12:47
zygomatique a écrit:salut
pour factoriser plus simplement le dénominateur ....
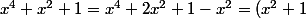^2 - x^2 = ....)
:lol3:
Effectivement

bien vu
-
zabata29
- Messages: 5
- Enregistré le: 02 Jan 2015, 22:44
-
 par zabata29 » 03 Jan 2015, 23:11
par zabata29 » 03 Jan 2015, 23:11
bonsoir, je bloque avec une autre primitive
PRIM(1/racine((2x-x^2)))dx
merci

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 04 Jan 2015, 12:14
par Ben314 » 04 Jan 2015, 12:14
C'est de nouveau du "classique" : il faut (encore...) mettre le trinôme du second degré sous forme canonique pour se ramener à un truc connu :
^2}}=\text{Arcsin}(x-1)+Cst)
(avec évidement
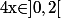
)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
zabata29
- Messages: 5
- Enregistré le: 02 Jan 2015, 22:44
-
 par zabata29 » 04 Jan 2015, 12:36
par zabata29 » 04 Jan 2015, 12:36
Ben314 a écrit:C'est de nouveau du "classique" : il faut (encore...) mettre le trinôme du second degré sous forme canonique pour se ramener à un truc connu :
^2}}=\text{Arcsin}(x-1)+Cst)
(avec évidement
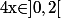
)
:mur: comment j'y ai pas pensé :marteau:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 68 invités
^2=\frac{1-\big(x^2\big)^3}{1-x^2}=\frac{(1-x^3)(1+x^3)}{(1-x)(1+x)}=(1+x+x^2)(1-x+x^2))
)
+Cst\) les deux suivant avec de l'arctangente une fois les dénominateurs mis sous forme canonique :
les deux suivant avec de l'arctangente une fois les dénominateurs mis sous forme canonique :^2+\frac{3}{4}}<br />=\frac{\frac{4}{3}}{\big(\frac{2x\pm 1}{\sqrt{3}}\big)^2+1}<br />=\frac{2}{\sqrt{3}}\times\frac{\frac{2}{\sqrt{3}}}{\big(\frac{2x\pm 1}{\sqrt{3}}\big)^2+1})
+Cst\)
