Dérivé n ieme
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
kurenay
- Membre Naturel
- Messages: 50
- Enregistré le: 09 Déc 2013, 23:44
-
 par kurenay » 23 Nov 2014, 15:41
par kurenay » 23 Nov 2014, 15:41
Bonjour,
Calculer la dérivé

de :
^n)
j'ai trouvé:
^n]^{(n)})
=
 +n(n-1) \times \frac{n!}{2}(1+x)^2)
Mais quand par exemple je remplace par n=3 dans mon expression,je retrouve pas le même résultat que quand je dérive 3fois
^3)
Merci de bien vouloir m'aider

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 23 Nov 2014, 15:48
par Ben314 » 23 Nov 2014, 15:48
Salut,
Tu as vu la formule permettant de dériver n fois un produit c'est à dire
^{(n)}=...)
?
Si oui, tu applique bêtement avec
=x^2\)
et
=(1+x)^n\)
:
^{(n)}(x)=\sum_{k=0}^n{n\choose k}f^{(k)}(x)g^{(n-k)}(x)=x^2g^{(n)}(x)+2nxg^{(n-1)}(x)+n(n-1)g^{(n-2)}(x))
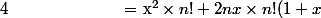+n(n-1)\times \frac{n!}{2}(1+x)^2)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 23 Nov 2014, 15:57
par Ben314 » 23 Nov 2014, 15:57
Salut,
Tu as vu la formule permettant de dériver n fois un produit c'est à dire
^{(n)}=...)
?
Si oui, tu applique bêtement avec
=x^2\)
et
=(1+x)^n\)
:
^{(n)}(x)=\sum_{k=0}^n{n\choose k}f^{(k)}(x)g^{(n-k)}(x)=x^2g^{(n)}(x)+2nxg^{(n-1)}(x)+n(n-1)g^{(n-2)}(x))
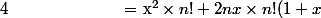+n(n-1)\times \frac{n!}{2}(1+x)^2)
Et... je trouve la même chose que toi...
(donc tu t'es gouré dans le cas n=3)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
kurenay
- Membre Naturel
- Messages: 50
- Enregistré le: 09 Déc 2013, 23:44
-
 par kurenay » 23 Nov 2014, 16:00
par kurenay » 23 Nov 2014, 16:00
Oui, j'ai utilisé la formule de Leibniz.
On pose
}=x^2)
}=2x)
}=2)
Et
}=n!)
}=n!(1+x))
}= \frac{n!}{2}(1+x)^2)
Puis j'ai placé les résultats dans la formule
} V^{(n)} + C_n^1 U^{(1)} V^{(n-1)} + C_n^2 U^{(2)} V^{(n-2)})
Ce qui donne le résultat que je vous ai envoyé précédemment
-
kurenay
- Membre Naturel
- Messages: 50
- Enregistré le: 09 Déc 2013, 23:44
-
 par kurenay » 23 Nov 2014, 16:01
par kurenay » 23 Nov 2014, 16:01
Ok d'accord Merci

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 23 Nov 2014, 16:03
par Ben314 » 23 Nov 2014, 16:03
Pour n=3, la formule "théorique" donne
+18(1+x)^2=60x^2+72x+18)
Et, "à la main", si tu dérive 3 fois
^3=x^5+3x^4+3x^3+x^2)
ça donne la même chose.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
kurenay
- Membre Naturel
- Messages: 50
- Enregistré le: 09 Déc 2013, 23:44
-
 par kurenay » 23 Nov 2014, 16:14
par kurenay » 23 Nov 2014, 16:14
Ah merci j'ai du faire une erreur de calcul :ptdr:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 47 invités