Théorème des résidus

[Ben314]

Peux -t-on intégrer une fonction sur un espace projectif pour avoir une sommation bornée ( i.e : ) ?

Si tu muni P1(R) d'une structure d'espace mesuré, tu peut (et c'est clairement faisable vu que P1(R) est homéomorphe au cercle trigo)

[barbu23]

Si tu muni P1(R) d'une structure d'espace mesuré, tu peut (et c'est clairement faisable vu que P1(R) est homéomorphe au cercle trigo)

C'est vrai ça ?
Comment munir d'une structure d'espace mesuré ?
Merci d'avance. :happy3:

[Ben314]

C'est vrai ça ?

Bien sûr que non : j'invente toutes les réponse au fur et a mesure que tu pose les question. :doh:

Comment munir d'une structure d'espace mesuré ?

Par transport de la structure d'espace mesuré du cercle trigo. via l'homéomorphisme.

[barbu23]

Je ne comprends pas pourquoi le cercle trigo possède une structure d'espaces mesurés.
Est ce que la surface de Boy se contracte en un point de l'espace ?

[Ben314]

Je ne comprends pas pourquoi le cercle trigo possède une structure d'espaces mesurés.

Parce qu'il est homéomorphe à [0,1]/{0=1}

Est ce que la surface de Boy se contracte en un point de l'espace ?

Tu as ne serait ce que ouvert l'article concernant la surface de Boy ?
Il y a dedans d'écrit que "Elle n'est pas plongeable dans un espace de dimension 3" donc... ta question n'a pas de sens.

[barbu23]

Tu as ne serait ce que ouvert l'article concernant la surface de Boy ?
Il y a dedans d'écrit que "Elle n'est pas plongeable dans un espace de dimension 3" donc... ta question n'a pas de sens.

J'ai dit "se contracte", c'est à dire "se rétracte" en un point et non "se prolonge". :happy3:

[Ben314]

J'ai dit "se contracte", c'est à dire "se rétracte" en un point et non "se prolonge". :happy3:

J'avais parfaitement compris.
Sauf que, avant de voir si un truc ou un bidule se "contracte" ou se "rétracte" dans R^3, il me semble que là première chose à regarder, c'est si le truc est ou pas une partie de R^3... :mur:

[barbu23]

J'avais parfaitement compris.
Sauf que, avant de voir si un truc ou un bidule se "contracte" ou se "rétracte" dans R^3, il me semble que là première chose à regarder, c'est si le truc est ou pas une partie de R^3... :mur:

Même si c'est pas une partie de , c'est à dire une partie qui contient , il peut se contracter pour devenir un partie de , non ? Peux tu me démontrer que c'est faux ?
Merci d'avance. :happy3:

Edit : Par exemple une sphère de dimension , privée de deux points antipodaux, peut se rétracter pour devenir un cercle de dimension .

[barbu23]

J'avais parfaitement compris.
Sauf que, avant de voir si un truc ou un bidule se "contracte" ou se "rétracte" dans R^3, il me semble que là première chose à regarder, c'est si le truc est ou pas une partie de R^3... :mur:

Même si c'est pas une partie de , c'est à dire une partie qui contient , il peut se contracter pour devenir un partie de , non ? Peux tu me démontrer que c'est faux ?
Merci d'avance. :happy3:

Edit : Par exemple une sphère de dimension , privée de deux points antipodaux, peut se rétracter pour devenir un cercle de dimension .

[Ben314]

Même si c'est pas une partie de , c'est à dire une partie qui contient .

Vu que le truc en question ne peut pas (10em édition) être vu comme une partie de , la question n'a pas de sens (bis et répétita...)

Par exemple une sphère de dimension , privée de deux points antipodaux, peut se rétracter pour devenir un cercle de dimension .

Oui, et c'est (visuellement et calculatoirement parlant) totalement évident.

[barbu23]

Vu que le truc en question ne peut pas (10em édition) être vu comme une partie de , la question n'a pas de sens (bis et répétita...)

Il me faut la preuve, car difficile de te croire. :happy3:

[SLA]

Il me faut la preuve, car difficile de te croire. :happy3:

Je trouve cette remarque un poil déplacée venant de toi.
Ta question n'étant déjà pas précise, on peut difficilement y répondre.
Enfin, quand bien même on te donne des preuves, il n'est pas dit que tu veuilles te donner le peine de les comprendre (voir le sujet le sinus en analyse complexe ).
Cordialement

[barbu23]

Non, mon français n'est pas toujours correcte. Je voulais dire sans preuve, difficile de croire ce qu'il dit, car je lui ai donné le contraire à ce qu'il affirme :
Une sphère à dimensions privé de deux points antipodaux peux se rétracter en un cercle de dimension .

[Ben314]

Une sphère à dimensions privé de deux points antipodaux peux se rétracter en un cercle de dimension .

Heuuuuu, c'est quoi le rapport avec la question ?

[Ben314]

Non, mon français n'est pas toujours correcte. Je voulais dire sans preuve, difficile de croire ce qu'il dit, car je lui ai donné le contraire à ce qu'il affirme :
Une sphère à dimensions privé de deux points antipodaux peux se rétracter en un cercle de dimension .

Ca m'intéresserait beaucoup que tu me dise quel rapport il y a entre le fait qu'une sphère privée de 2 points se contracte en un cercle et la question qu'on se pose sur P2(R) ?
Ou, si tu préfère, en quoi ton truc est sensé être "le contraire de ce que j'affirme" ?

[barbu23]

Voici comment je vois les choses : ( ça peut être faux, c'est pourquoi je demande une preuve à vos affirmations )
se plonge par homéomorphisme dans , donc : s'identifie à une sous variété réelle de . Donc, on peut tout simplement dire que : est une sous variété de , non ?
Donc un objet quelconque de peut se rétracter pour donner un objet de , non ? Je ne sais pas le prouver mais j'ai donné un exemple qui illustre ça :
Une sphère de dimension deux privée de deux points antipodaux peuvent se rétracter pour donner un cercle, donc un objet de dimension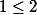 , non ?
Il se peut que je raconte n'importe quoi, car je ne maîtrise pas très bien ces choses là. :happy3:

Cordialement. :happy3:

[barbu23]

Il y'a un truc qui ne marche pas dans ce que j'ai dit. :hum:
Mais, je reçois d'abord votre réponse pour voir si on peut se mettre d'accord sur certains points. :happy3:

[Ben314]

Donc un objet quelconque de peut se rétracter pour donner un objet de , non ?

Si par rétraction, tu entend "rétraction continue", non, on ne peut pas, pas plus qu'on ne peut "rétracter" P^2(R) sur R^2, ni P^1(R) sur R (dans le dernier cas c'est totalement trivial: on ne peut pas rétracter un cercle sur un cercle privé d'un point)

Il se peut que je raconte n'importe quoi, car je ne maîtrise pas très bien ces choses là.

Possible... :zen:

[barbu23]

La question était de savoir si :

Est ce que la surface de Boy se contracte en un point de l'espace

?

[barbu23]

Un petit up pour voir si quelqu'un peut me répondre. :happy3:
Merci d'avance. :happy3: