J'aurai aimé savoir calculer cette somme à l'aide du théorème des résidus.
Par quoi faut-il démarrer ? ??
Calcul de somme à l'aide du théoreme des résidus
12 messages
- Page 1 sur 1
Calcul de somme à l'aide du théoreme des résidus
par sky-mars » 06 Juin 2009, 14:45
Bonjour tout le monde !
J'aurai aimé savoir calculer cette somme à l'aide du théorème des résidus.
^{n}}{(2n+1)^{3})
Par quoi faut-il démarrer ? ??
J'aurai aimé savoir calculer cette somme à l'aide du théorème des résidus.
Par quoi faut-il démarrer ? ??
par sky-mars » 07 Juin 2009, 08:08
lol si j'aurai preféré , ouais j'aurai preferé , sauf que l'énoncé m'impose de passer par le théoreme des résidus .
Et puis , il semble qu'avec les séries de fouriers on peut que calculer les termes paires .
Et puis , il semble qu'avec les séries de fouriers on peut que calculer les termes paires .
par yos » 07 Juin 2009, 08:23
Comme ça je vois pas d'intégrale qui donnerait la série.
Avec les séries de Fourier, ça marche en prenant par exemple
=x(\pi-x))
sur 
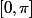
impaire et 
-per.
Avec les séries de Fourier, ça marche en prenant par exemple
par sky-mars » 07 Juin 2009, 08:33
On me dit d'utiliser
une fonction du type}{sin(\pi z)})
avec le théoreme des résidus et de trouver la fonction f adéquates mais franchement je seche complétement.
une fonction du type
par sky-mars » 07 Juin 2009, 10:06
comment on peut démontrer que
par Nightmare » 07 Juin 2009, 11:27
Salut :happy3:
Tu as essayé simplement de passer au module? :lol3:
Sinon, on pose effectivement=\frac{\pi f(z)}{sin(\pi z)})
avec =\frac{1}{(2z+1)^{3}})
f est méromorphe sur
.
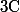
En écrivant le développement en série de Laurent du sinus et sachant que les pôles de f ne sont pas entiers, on a rapidement :
=\{{f(z) si z\in \mathbb{Z}\\Res_{z_{0}}(f)\pi sin(\pi z) sinon)
Si je note
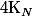
le carré que tu considères à 11h06, on a alors d'après le théorème des résidus :
dz\;\;=\;\;\Bigsum_{n\in [|-N,N|]} (-1)^{n}f(n)\;+\;\Bigsum_{z_{0}\in K_{n}} Res_{z_{0}}(f) \pi sin(\pi z))
Continue.
:happy3:
Tu as essayé simplement de passer au module? :lol3:
Sinon, on pose effectivement
f est méromorphe sur
En écrivant le développement en série de Laurent du sinus et sachant que les pôles de f ne sont pas entiers, on a rapidement :
Si je note
Continue.
:happy3:
par sky-mars » 07 Juin 2009, 19:34
bon finalement j'ai trouvé comment il fallait faire :
je me suis servit de})
Le pôle de cette fonction c'est
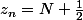
}, z_{n}) = (-1)^{n+1})
Puis j'utilise une fonction f adéquate pour qu'on ait
}{cos(\pi z)})
(*) qui soit nulle sur le contour rectangulaire que j'ai proposer à 11h06
Ici j'ai pris= \frac{1}{z^3})
d'une part on a
 , z_{n} ) = \frac{8(-1)^{n+1}}{(2n+1)^3})
et
, 0 ) =\frac{\pi^3}{2})
on a quand
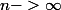
}{cos(\pi z)} dz = 0 = 2i\pi (\sum\limits_{n=-\infty}^{\infty} \frac{8(-1)^{n+1}}{(2n+1)^3} + \frac{\pi^3}{2})
)
^{n}}{(2n+1)^3} =\frac{\pi^3}{2})
^{n}}{(2n+1)^3} =\frac{\pi^3}{32})
AQT
et voila 
je me suis servit de
Le pôle de cette fonction c'est
Puis j'utilise une fonction f adéquate pour qu'on ait
Ici j'ai pris
d'une part on a
et
on a quand
AQT
et voila
12 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 77 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :