Bonjour je suis en prepa HEC, et je bloque sur certaines questions de mon DM.
On a la fonction 1- racine(x²+1)
f(x)= _____________
x
DF= R*, on a trouver la limite en 0 par prolongement par continuité, cette limite est 0
1) On me demande maintenant de trouver la limite du taux d'accroissement en 0,or je tombe sur une forme indeterminée et je ne vois pas par ou commencer.
lim f(x)-f(0) / x-0 = FI
0
pouvez vous me donner des pistes...
2) on me demande de montrer que pout tout x>0 f(x) = (1/x)- racine (1+ (1/x²))
J'ai cherché cette question en utilisant la forme conjuguée or je suis bloquée a la fin pouvez vous m'aider !!
je vous remercie par avance pour votre aide !!
Des pistes svp !! DM pour lundi
5 messages
- Page 1 sur 1
hey_laine a écrit:Bonjour je suis en prepa HEC, et je bloque sur certaines questions de mon DM.
On a la fonction 1- racine(x²+1)
f(x)= _____________
x
DF= R*, on a trouver la limite en 0 par prolongement par continuité, cette limite est 0
1) On me demande maintenant de trouver la limite du taux d'accroissement en 0,or je tombe sur une forme indeterminée et je ne vois pas par ou commencer.
lim f(x)-f(0) / x-0 = FI
0
pouvez vous me donner des pistes...
2) on me demande de montrer que pout tout x>0 f(x) = (1/x)- racine (1+ (1/x²))
J'ai cherché cette question en utilisant la forme conjuguée or je suis bloquée a la fin pouvez vous m'aider !!
je vous remercie par avance pour votre aide !!
salut
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
bonjour,
pour résoudre les formes indéterminées "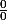 ", trois outils:
", trois outils:
i) le taux d'accroissement-f(0)}{x})
qui se résoud en f'(0)
exemple}{x} = (ln)'(1)=1/1=1)
ii) le théorème de L'Hospital
}{g(x)}=\lim_{x \rightarrow0} \, \frac{f'(x)}{g'(x)})
si=g(0)=0) et f ,g de classe C1 ((à dérivée continue)
et f ,g de classe C1 ((à dérivée continue)
exemple
-x}{cos(x)-1}=\lim_{x \rightarrow 0} \frac{cos(x)-1}{-sin(x)}=\lim_{x \rightarrow 0} \, \frac{-sin(x)}{-cos(x)}=0)
iii) enfin, remplacer l'image f(x) (resp g(x)) par un développement limité,ie,par
un polynome qui indique le comportement local de f(x):
par exemple, dans un voisinage de x=0,
on peut remplacer sin(x) par)
ii) pour la (2), il suffit de faire rentrer "x" dans la racine sous forme de
dans ce sens, ça ne pose aucun problème. c'est l'inverse qui est dichotomique
puisque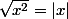 avec discussion pour simplifier.
avec discussion pour simplifier.
pour résoudre les formes indéterminées "
i) le taux d'accroissement
qui se résoud en f'(0)
exemple
ii) le théorème de L'Hospital
si
exemple
iii) enfin, remplacer l'image f(x) (resp g(x)) par un développement limité,ie,par
un polynome qui indique le comportement local de f(x):
par exemple, dans un voisinage de x=0,
on peut remplacer sin(x) par
ii) pour la (2), il suffit de faire rentrer "x" dans la racine sous forme de
dans ce sens, ça ne pose aucun problème. c'est l'inverse qui est dichotomique
puisque
mathelot a écrit:pour la (1), tu peux écrire également:
puisque le taux d'accroissement a pour limite , le nombre dérivé en x=0, de
pour la 1/ la quantité conjuguée suffit aussi ... mais reconnaître un taux de variation est toujours appréciable ....
:lol3:
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
5 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 64 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
