Pistes pour une récurrence ?
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Aldebaran
- Membre Naturel
- Messages: 41
- Enregistré le: 03 Aoû 2005, 11:36
-
 par Aldebaran » 20 Aoû 2005, 17:31
par Aldebaran » 20 Aoû 2005, 17:31
Bonjour à tous !
J'ai essayé de montrer la relation suivante par récurrence sur

mais je vous avoue que je ne suis pas sûr de mon résultat (notament en ce qui concerne le changement d'indice à un moment donné).
Est-ce-que quelqu'un aurait une idée, ou une piste ?
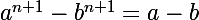 \sum _{k=0}^n a^{n-k}b^{k})
-
dilzydils
- Membre Relatif
- Messages: 140
- Enregistré le: 02 Aoû 2005, 14:43
-
 par dilzydils » 20 Aoû 2005, 17:42
par dilzydils » 20 Aoû 2005, 17:42
Il manque (a-b) devant sigma non??
-
Aldebaran
- Membre Naturel
- Messages: 41
- Enregistré le: 03 Aoû 2005, 11:36
-
 par Aldebaran » 20 Aoû 2005, 22:11
par Aldebaran » 20 Aoû 2005, 22:11
Effectivement, autant pour moi !
Je corrige sur l'original...
-
Evariste
- Messages: 6
- Enregistré le: 17 Aoû 2005, 16:11
-
 par Evariste » 21 Aoû 2005, 00:22
par Evariste » 21 Aoû 2005, 00:22
:id:
Voilà un début de solution qui aboutit (heureusement !!!) et qui ne fait pas intervenir de changement d'indice.
Naturellement, la relation est vraie pour

.
Hypothèse de récurrence au rang

:
[center]

.
[/center]
A partir de là, tu utilises ton HR

pour écrire :
[center]

.
[/center]
Il ne reste plus qu'à multiplier par

les deux membres de cette dernière égalité, et à transformer le membre de droite obtenu pour vérifier l'HR

.
:zen:
-
Aldebaran
- Membre Naturel
- Messages: 41
- Enregistré le: 03 Aoû 2005, 11:36
-
 par Aldebaran » 21 Aoû 2005, 16:49
par Aldebaran » 21 Aoû 2005, 16:49
J'essaye depuis 1/2 heure de suivre cette voie mais j'avoue ne pas réussir à boucler le raisonnement...
On multiplie donc par
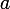
chaque membre de l'égalité, on retombe sur :
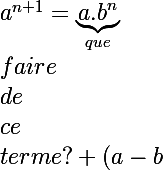. \sum _{k=0}^{n-1} \large {a^{n-k}.b^{k}})
.
Et là je suis bloqué (j'ai honte...)
Je n'arrive pas, d'une part à faire entrer ce terme sous une somme et d'autre part à faire apparaître le rang

-
Evariste
- Messages: 6
- Enregistré le: 17 Aoû 2005, 16:11
-
 par Evariste » 21 Aoû 2005, 16:58
par Evariste » 21 Aoû 2005, 16:58
Tout simplement en ajoutant et en retranchant

dans le membre de droite ! Après tu factorises

en

, ce qui te donnes le terme pour

manquant dans la somme, et je te laisse conclure ! :we:
-
Galt
- Membre Rationnel
- Messages: 789
- Enregistré le: 13 Aoû 2005, 12:03
-
 par Galt » 21 Aoû 2005, 17:00
par Galt » 21 Aoû 2005, 17:00
Astuce :
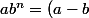b^n+b^{n+1})
et ça baigne.
-
Aldebaran
- Membre Naturel
- Messages: 41
- Enregistré le: 03 Aoû 2005, 11:36
-
 par Aldebaran » 21 Aoû 2005, 17:02
par Aldebaran » 21 Aoû 2005, 17:02
Thanks for jour help.
I'm enjoy to be here with you !!!
:ptdr:
-
Evariste
- Messages: 6
- Enregistré le: 17 Aoû 2005, 16:11
-
 par Evariste » 21 Aoû 2005, 17:07
par Evariste » 21 Aoû 2005, 17:07
De nada ! :zen:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 18 invités
 .
. :
:  .
. pour écrire :
pour écrire : .
. les deux membres de cette dernière égalité, et à transformer le membre de droite obtenu pour vérifier l'HR
les deux membres de cette dernière égalité, et à transformer le membre de droite obtenu pour vérifier l'HR .
.