Question

[fatal_error]

bj,

je suis un peu mitigé, par exemple la résolution d'une equation..
x^2 - 2x +1 = 0 (x-1)^2=0
=> x = 1
Le fait que x^2-2x+1=0 implique que x == 1, on a utilisé implique et pourtant ca n'a rien d'un théorême...

alors oui, ptet faut écrire les solutions de lequation blabla sont Sx={1}, mais bon, jvois pas le malaise!

[Joker62]

J'ai toujours apprécié ce petit papier :

http://bkristof.free.fr/methodologie/Petit%20manuel%20de%20bonne%20redaction.pdf

[fatal_error]

hello,

petite question:
pourquoi faut pas dire que f(x) est dérivable pour tout x appartient à R, mais faut dire f(x) est dérivable sur R?

[paquito]

Bonjour Fatal_ error,

La résolution des équations est un cas particulier, puisque l'on peut souvent procéder par équivalences et l"" pose beaucoup moins de problème; d'autre part une équation est une phrase supposée vrai, donc on travaille avec p supposé vrai et on passe d'une équation à une équation équivalente et si on aboutit à 0=3, on peut conclure que l'équation de départ qui a la même valeur de vérité ne peut avoir de solution.

Par contre si l'on écrit cela prouve que l'ensemble des solutions de (x-1)^2=0 est inclus dans l'ensemble des solutions de , ce qui veut dire que s'il y a une solution, c'est 1, mais il faut logiquement vérifier que 1 est effectivement solution et si l'on procède par implication, on doit réciproquement prouver que les solutions trouvées le sont effectivement.

De toutes façons, on est parfois obligé de procéder par implication:exemple

Soit à résoudre sur ); dans un premier temps on démontre:

et , puis il faut ensuite déterminer les réels effectivement solutions; il y en a 4 parmi une infinité!

Avant de conclure, prenons l'exemple suivant , cette fois ci l'implication est fausse car sinon les 2 équations seraient équivalentes donc ce qui est écrit est faux; pas facile d'expliquer pourquoi!

En conclusion, les équations posent moins de problèmes et parfois on ne peut pas faire autrement; toutefois si l'on peut procéder par équivalence, c'est mieux puisque ça évite une réciproque qui ne sera pas comprise.

[paquito]

hello,

petite question:
pourquoi faut pas dire que f(x) est dérivable pour tout x appartient à R, mais faut dire f(x) est dérivable sur R?

Et c'est quoi la définition de f est dérivable sur R? Pour la première phrase, la négation est difficile à écrire, il faudrait faire la distinction entre existe et existe , , mais comme les quantificateurs ne sont pas au programme, pour moi les deux phrases sont acceptables, même si je trouve la seconde moins maladroite. Visiblement, il n'y a pas d'ambiguïté ni d'erreur de logique.

[paquito]

J'ai toujours apprécié ce petit papier :

http://bkristof.free.fr/methodologie/Petit%20manuel%20de%20bonne%20redaction.pdf

Bonjour Joker62,

et merci pour ton lien qui me rassure quand même; pendant un moment j'ai pensé que maintenant on faisait des maths en bafouant toute règle de logique; tout se barre!

[beagle]

Bonjour Joker62,

et merci pour ton lien qui me rassure quand même; pendant un moment j'ai pensé que maintenant on faisait des maths en bafouant toute règle de logique; tout se barre!

ça ne se barre pas puisqu'on faisait pas ch..er avec ça de mon temps au lycée.
Alors que cela une instruction pour les études de maths à partir de bac plus je sais pas quoi,
ben autant le préciser à ce moment là.

Parce que au collège et au lycée.
On prend un p qui est dans l'énoncé, regarde les exos, on part de l'énoncé.
Et donc je le répète le jour où l'énoncé du problème 13 page 57 est faux, c'est le lendemain dans l'exo 17 de la page 59.
p est vrai puisque c'est ce que l'on nous dit de prendre.

Ensuite il existe des exos où comme tu le dis on est en équivalence,
genre démontrer que formule A = formule B
ben partir de a pour arriver à B,
franchement on se fout de quand A est faux...

ensuite des exos démontrer que "patati".
là départ en blanc, à votre bon coeur.
ben à partir de quoi l'élève doit-il partir?
a partir de présupposé (vrai) de son niveau.

Maintenant le jour où l'élève fait p implique p' implique p" implique q avec du p qui est faux,
j'ai tout compris je crois, dites moi si c'est cela,
je lui fais réécrire p donc p' donc p" donc q.
Argh!
Les deux démonstrations sont fausses et point barre.
suffit d'entourer p et de dire à l'élève, c'est bien mais revient quand p sera vrai.
et faire ch..er uniquement l'élève dans cette situation.

[paquito]

Bonjour ingrid55,

Tu as raison, la démonstration par l'absurde est parfois très délicate; en plus on distingue la vraie démonstration par l'absurde ou l'on finit par p et non p sont vraies, c'est à dire qu'on nie le principe du tiers exclus (une proposition est exclusivement vraie ou fausse), la plus célèbre est celle-ci:

Soit un ensemble; il n'existe pas de surjection de dans .

Démonstration: soit Soit un ensemble et une surjection de dans et posons:

{} ,et soit 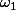un antécédent de ;

Soit mais alors ;

Soit mais alors ; la proposition

est à la fois vraie et fausse, ce qui contredit le principe du tiers exclus;

par conséquent n'existe pas.

Voilà donc ce qu'on appelle une vraie démonstration par l'absurde; il en existe d'autres, mais ça devient vite compliqué et celle ci est très importante (elle permet par exemple démontrer que n'est pas en bijection avec.


Pour les autres démonstrations par l'absurde, on veut montrer qu'une implication p=>q est vraie; on suppose que p est vraie et q est fausse, et on aboutit à une contradiction sur p, mais on a démontré que non q=>non p; on a donc en fait démontré une contraposée, d'où l'appellation de fausse démonstration par l'absurde; (c'est quand même une démonstration par l'absurde car on aboutit à une contradiction.

En ce qui concerne la géométrie dans l'espace, il y a déjà un bout de temps, on l'enseignait dès la classe de seconde en utilisant quelques propriétés d'incidence, puis en démontrant tout par l'absurde!
Même en temps que prof, on avait intérêt à réviser les démonstrations sous peine de panne sèche!

La première démonstration du cours, après avoir donné les quelques propriétés admise, était:

Soient, et 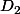3 droites de l'espace; on suppose

et , montrer que 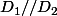; déjà, personne ne comprenait pourquoi on voulait démontrer un résultat évident et le prof savait que sa démonstration par l'absurde ne serait pas comprise (on avait tout faux d'avance!)

Il fallait déjà démontrer que et 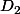n'avaient aucun points en commun; pour cela on utilisait les plans défini par et
et défini par et 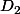et on montrait que si et 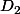avaient un point en commun alors et seraient confondus ce qui est absurde puisqu'on parlait de // strict( je résume bien sûr); arrivé là, il fallait essayer de convaincre l'auditoire que ce n'était pas fini; mais l'auditoire avait décroché depuis longtemps;

donc on terminait tout seul à démontrer que et 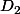étaient coplanaires avec encore une belle démonstration par l'absurde, pour le coup complètement absurde.

Je t'ai fait un rapide résumé, mais ça prenait l'heure; et commencer à faire des démonstrations par l'absurde difficiles, c'est pédagogiquement stupide; les élèves rejetant en masse et la géométrie dans l'espace et le raisonnement.

Donc je te comprends très bien, si tu as eu à subir ce genre de cours inutile et néfaste!

[beagle]

Je sais pas en fait pourquoi on m'a désigné pour contrarier paquito.

Deux droites perpendiculaires D1 et D2 à une troisième droite D3 sont parallèles.

ben si elles ne sont pas parallèles, elles se coupent en I.
on note A et B les points de D1 et D2 qui coupent D3.

Alors la somme des angles du triangle ABI est 90° + 90° + la valeur de l'angle AIB,
ce qui donne un triangle dont la somme des angles dépasse 180°.
Ce n'est pas possible, donc I n'existe pas, etc...

bien sur tout n'est pas rose et acceptable,faut savoir quelles notions sont antérieures ou non, etc..., mais bon,
perso j'adore les démonstrations par l'absurde.
Si Paquito avait raison on irait dans le décors, donc paquito a amicalement tort.

[Mikihisa]

Dans l'espace deux droite peuvent très bien ne pas être // et pourtant ne jamais se couper :)

[beagle]

Dans l'espace deux droite peuvent très bien ne pas être // et pourtant ne jamais se couper

vi, vi, on écrit vite aussi.

tiens pendant que tu es là:
si j'écrits
ABCD carré implique angle ABC 90°
c'est faux,
c'est ça, faut rajouter et ABCD est un carré.
c'est ça?

[Mikihisa]

:D cette grogne !

Tiens pendant qu'on parles de géométrie : trouvez vous acceptable cette définition :
1) un point est l'intersection de deux droites

[beagle]

:D cette grogne !

Tiens pendant qu'on parles de géométrie : trouvez vous acceptable cette définition :
1) un point est l'intersection de deux droites

de deux droites sécantes, ou l'intersection de deux droites non sécantes?

[paquito]

re beagle,

Dans l'espace, 2 droites perpendiculaires sont sécantes, donc ta démo est valables quand les 3 droites sont coplanaires; si tu prend comme hypothèse: D_1 orthogonale à D_3 et D_2 orthogonale à D_3, ta démo ne tient plus; dessine un cube ABCDEFGH collé à un cube BC'D'CFF'G'G (désolé, je ne sait pas insérer la figure), tu as (BF) orthogonale à (GH) et (BF) orthogonale à (C'D') et en fait (GH) est orthogonale à(C'D'), donc dans l'espace, c'est plus compliqué que dans le plan; j'aurais même pu faire plus simple: dans ABCDEFGH, on a (BF) perpendiculaire à (BD), (BF) orthogonale à(GH) et (BD) et (GH) ne sont pas//; pire! (BF) perpendiculaire à(BD); (BF) perpendiculaire à (BC) et (BD) n'est pas // à (BC); donc il n'y a vraiment plus rien qui marche!! Sinon, en dimension 2, ta démo est tout à fait valable et donne un exemple très abordable de démo par l'absurde.

[paquito]

:D cette grogne !

Tiens pendant qu'on parles de géométrie : trouvez vous acceptable cette définition :
1) un point est l'intersection de deux droites

Si on définit correctement une droite avant?!?! la droite est un ensemble de points alignés?!?!
En fait, c'est avec la notion d'espace affine que ça marche le mieux, mais il faut avoir vu la notion d'espace vectoriel avant(, et ), mais de toutes façons, tu abordes un problème difficile. il y a aussi une construction axiomatique
mais les élèves ne posant jamais la question, ça ne me semble pas utile de les perturber.

Donc pour moi définir un point comme l'intersection de 2 droites, on se mord la queue mais dire que l'intersection de 2 droites peut être un point, bien sûr, même si au temps des maths modernes on écrivait ={}.

[paquito]

J'insiste encore une fois,

Soit ABCD un parallélogramme non-rectangle; si j'écris: , j'écris une proposition qui est vraie, mais complètement inutilisable; j'aurais pu écrire: "Paris capitale de la Belgique=>Bruxelles capitale de l'italie", proposition qui est vraie, mais qui ne sert strictement à rien. La première implication serait utilisable si ABCD était un rectangle, ce qui n'est pas le cas, donc pour utiliser une proposition "p=>q" il faut auparavant avoir prouvé (où c'est une hypothèse) que p est vrai; donc ce n'est pas parce que "p=>q" est vraie que ça prouve quoi que ce soit, encore moins que q est vraie.

Voilà, j'ai l'impression d'être un vieux prof archaïque, hyper pointilleux et qui ne supporte pas la moindre faute de ponctuation dans une démonstration, alors que plus cool que moi,c'est rare.

Par exemple, si un élève doit déduire le signe de f(x) alors que dans la question précédente on montre que f(x) s'écrit comme somme de deux carrés et qu'on a aussi la courbe représentative de f, je mets le maximum lorsque je vois f(x)>0, même s'il n'y a aucune justification. (De toutes façons il y a 7 élèves sur 35 qui répondent).

Par contre, je n'utilise jamais l'implication (réservée aux sup et aux spé) et je continue de souligner les fautes d'orthographes (sans bien sûr les pénaliser) et je leur rappelle qu'il y a des conjonctions de coordination. Quant à faire cours en langage SMS; jamais!!

[beagle]

J'insiste encore une fois,

Soit ABCD un parallélogramme non-rectangle; si j'écris: , j'écris une proposition qui est vraie, mais complètement inutilisable; j'aurais pu écrire: "Paris capitale de la Belgique=>Bruxelles capitale de l'italie", proposition qui est vraie, mais qui ne sert strictement à rien. La première implication serait utilisable si ABCD était un rectangle, ce qui n'est pas le cas, donc pour utiliser une proposition "p=>q" il faut auparavant avoir prouvé (où c'est une hypothèse) que p est vrai; donc ce n'est pas parce que "p=>q" est vraie que ça prouve quoi que ce soit, encore moins que q est vraie.

Voilà, j'ai l'impression d'être un vieux prof archaïque, hyper pointilleux et qui ne supporte pas la moindre faute de ponctuation dans une démonstration, alors que plus cool que moi,c'est rare.

Par exemple, si un élève doit déduire le signe de f(x) alors que dans la question précédente on montre que f(x) s'écrit comme somme de deux carrés et qu'on a aussi la courbe représentative de f, je mets le maximum lorsque je vois f(x)>0, même s'il n'y a aucune justification. (De toutes façons il y a 7 élèves sur 35 qui répondent).

Par contre, je n'utilise jamais l'implication (réservée aux sup et aux spé) et je continue de souligner les fautes d'orthographes (sans bien sûr les pénaliser) et je leur rappelle qu'il y a des conjonctions de coordination. Quant à faire cours en langage SMS; jamais!!

argh, mais vas-tu répondre alors à ce que je demande depuis x pages.
On a un problème avec un énoncé soit le carré ABCD ,soit ..., montrez que...
pourquoi ne puis-je pas dire:
ABCD carré implique angle ABC vaut 90°
suis-obligé de dire et ABCD est un carré car comme le port salut c'est écrit dans l'énoncé?

[paquito]

argh, mais vas-tu répondre alors à ce que je demande depuis x pages.
On a un problème avec un énoncé soit le carré ABCD ,soit ..., montrez que...
pourquoi ne puis-je pas dire:
ABCD carré implique angle ABC vaut 90°
suis-obligé de dire et ABCD est un carré car comme le port salut c'est écrit dans l'énoncé?

Si l'énoncé précise que tu as un carré, tu as juste à dire ABCD étant un carré puis tout ce que tu peux en déduire (diagonales, angles, etc), mais tu doit le préciser même si là il n'y a aucune démonstration; il faut absolument dire que p est vraie pour pouvoir appliquer p=>q; c'est une règle fondamentale de logique. si tu écrit directement AC=BD, tu auras comme remarque: pourquoi? c'est normal, car l'énoncé peut être complexe et dans ce que tu écris, il n'y a aucune déduction mais une affirmation gratuite; c'est exactement comme si dans un raisonnement par récurrence, tu n'écrivais pas l'hypothèse de récurrence, mais que tu l'utilisais quand même: tu aurais comme remarque: d'où ça sort? et une implication n'a jamais été une déduction!

Ceci dit, je commence à être fatigué de répéter l'évidence; il y a un lien sur ce forum on sont clairement données les règles de rédaction. Moi, j'abandonne.

[Mikihisa]

On se mord la queue en effet si on définie le point a partir de la droite et la droite a partir du point :/

Me semble justement que Euclide (il s'agit du paradoxe d'Euclide) définissait alors le point comme étant "ce que l'on ne peux pas scinde" ou encore "ce qui n'a pas de partie".

[Ingrid55]

Ce sujet dérive beaucoup trop . L'important est de connaitre les grandes lignes , et certains cas particuliers . Mais c'est vrai que l’apprentissage des symboles devrait être plus explicité par des phrases et vice-versa ... On ne peut pas toujours tout remettre en doute en maths .