Exercice d analyse 1s

[zygomatique]

En elevant au carré f et g sans en passer par la dérivée on se retrouve avec ce qui après simplification n'ait guère mieux pour démontrer l'inégalité . Peut être faut il prendre l'enoncé dans son ensemble et se cantonner à l'encadrement

un peu de sérieux ::

4x^3 - x^4 = x^3(4 - x) et le signe est trivial ....

[Shew]

un peu de sérieux ::

Haha!!! oui en y reflechissant, 4 - x positif pour donc

pour donc il vallait mieux ne pas utiliser les dérivés .

Désolé sur le coup j'avais pas vue cela donc soyez pas faché merci prof :lol3:

[zygomatique]

pas faché du tout ...

juste te rappeler que le calcul doit servir à quelque chose .... et si on oublie l'objectif alors on croit être coincé alors qu'il n'en est rien ici ....

:lol3:

[Shew]

pas faché du tout ...

juste te rappeler que le calcul doit servir à quelque chose .... et si on oublie l'objectif alors on croit être coincé alors qu'il n'en est rien ici ....

:lol3:

Promis chef , j'essaierai de m'y tenir à l'avenir :lol3: . J'espere avoir pu aider la personne qui en avait besoin .

[Ingrid55]

Oui , la réponse parait un peu nase maintenant ^^! @zygo avait parlé de cette technique dans un autre topic auquel j'y ai participé .
Mais ce serait plus difficile si l'intervalle était différente , il pourrait y avoir un autre encadrement ...

[paquito]

L'intérieur d'une racine est toujours positive et tu sais que racine de 0 n'existe pas , d'ailleurs ici (-x^2 + 4x + 4) = (-x + 2)^2 .

Mais que désigne le "?'" au niveau du numérateur ? il faudrait mettre la puissance ...

Racine de 0 n'existe pas???

[Ingrid55]

oui je sais , c la première qu'on apprend sur la racine :zen:
Mais s'il y'avait une autre expression ...(mais là c'est un autre exo à voir) .

[paquito]

donc f,g et h sont positives et même f(0) = g(0) = h(0) = 2

or

et

on fait la différence et on factorise par x^2 et alors il ne reste que le signe d'un trinome du second degré dont le signe est aisé ...

idem pour f et h ... en à peine plus dure ... :zen:

:lol3:

au fait quelles sont les variations de f, g et h sur [0, 2] ?

Réponse: f,g et h sont positives depuis longtemps
le problème est aussi résolu depuis longtemps!

[Ingrid55]

Oui , voilà .

[Shew]

Réponse: f,g et h sont positives depuis longtemps

En effet mais avec les dérivées, f, g et h se sont un peu noyées :we:

[paquito]

En fait, montrer que f, g et h sont positives sur [0; 2] se fait très facilement; il y a le fait que f(0)=g(0)=h(0) et f'(0)=g'0)=h'0) qui aurait pu être exploité ; peine perdu il fallait calculer ce qui donnait, donc pas de problème et qui donnait , qui là non plus ne posait pas de problème.

Finalement, pas l'ombre d'une subtilité, que du calcul et tout ça pour encadrer f(1/10000)alors que pour trouver 1/10000 on avait besoin d'utiliser la touche , sauf intuition exceptionnelle?

Donc du calcul lourd et pas du tout dans l'esprit du programme pour un but très critiquable.

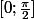
Il y a quand même des exemples plus intéressants: si on prend les fonctions f, g et h définies sur par , et , on a donc puisque et que , et le même raisonnement conduit finalement à ;

c'est quand même plus intéressant que du calcul bourrin! où alors de se limiter pour |x|<1 à établir que
. pour 1+x=0,999,
ce qui donne, ce qui montre l'intérêt et on peut faire plusieurs expérience.

En conclusion, l'exercice dont il a été question ne sera jamais donné à mes élèves.

[nour2013]

salut
comment peux ton exploiter le fait que f(0)=g(0)=h(0) et f'(0)=g'0)=h'0) .

merci bien

[paquito]

On a et sur, donc
sur ; ensuite, sur , donc est croissante sur ; comme, sur et enfin, et sur , donc h est croissante sur , et , ce qui donne sur et comme sur on a, finalement, sur , on a :



Errata: j'avais écris g au lieu de h.

[zygomatique]

salut
comment peux ton exploiter le fait que f(0)=g(0)=h(0) et f'(0)=g'0)=h'0) .

merci bien

les trois courbes ont la même tangente au point d'abscisse 0 ...

[paquito]

les trois courbes ont la même tangente au point d'abscisse 0 ...

oui, mais au moins ça demande un peu de raisonnement!

[zygomatique]

oui, mais au moins ça demande un peu de raisonnement!

absolument pas ::

une tangente est définie par f(a) = b et f'(a) = c

ici f(0) =g(0) = h(0) et f'(0) = g'(0) = h'(0)

épictou ...

[paquito]

absolument pas ::

une tangente est définie par f(a) = b et f'(a) = c

ici f(0) =g(0) = h(0) et f'(0) = g'(0) = h'(0)

épictou ...

Il y a plein d'exercice où f(x)<g(x) passe par l'étude de d(x) =f(x)-g(x) et où on ne peut pas faire un étude directe bête et méchante: exemple ln(1+x) et x pour -1<x<1; on peut quand même sortir de l'exercice sans intérêt! sors un peu!

[zygomatique]

no comprendo ... :doh: