Marche aléatoire

[Alicia26]

Bonjour à tous, je suis bloqué sur une preuve à priori toute bête, mais je bloque depuis un moment, je vous demande alors votre aide :

Soit U_n la matrice ligne associée à une marche aléatoire n.
Si M est la matrice transition alors U_n+1= U_n M.

On note U_n = (P(Xn=S1, ... P(Xn)=S_N ) ( matrice ligne )

J'ai réussi à le montrer pour le cas où on a seulement deux états avec les propabilités totales, j'ai calculé P(Xn+1=S1) et P(Xn+1=S2) et j'en ai déduit le théorème.

Cas général : Je ne me vois pas calculer tout les P(Xn+1= S1 ) ... P(Xn+1=S_N)
peut être une récurrence.

Merci de m'aider à démarrer :happy2:

[Alicia26]

Un petit coup de pouce svp :mur:

[Ben314]

Salut,
Je ne pense pas être le seul à avoir lu ton post et... à n'avoir pas compris où résidait la question.
Lorsque tu écrit "...j'en ai déduit le théorème.", tu parle de quel théorème ?

S'il s'agit du fait que où est la matrice de transition, c'est pas franchement ce que j'appellerais un "théorème", mais plutôt une définition (celle du terme "matrice de transition").

Et en ce qui concerne l'existence d'une telle matrice (avec des coefficients constant), elle résulte de la définition même d'une "marche aléatoire" qui te dit que toute les proba conditionnelles (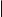="sachant que") ne dépendent que de et et pas de .

Donc , et le fait que , c'est simplement la bête formule dite "des proba. totales" :

[Alicia26]

Ah oui merci, effectivement j'ai oublié de cité le théorème :

Alors le théorème est :

Soit Un la matrice ligne Un=(P(Xn=S1) .... P(Xn=Sn)) associé à une marche aléatoire à l'instant n.

Si M est sa matrice de transition alors Un+1=Un*M et Un=U0*M

Voila merci de m'aider.

[DamX]

Ah oui merci, effectivement j'ai oublié de cité le théorème :

Alors le théorème est :

Soit Un la matrice ligne Un=(P(Xn=S1) .... P(Xn=Sn)) associé à une marche aléatoire à l'instant n.

Si M est sa matrice de transition alors Un+1=Un*M et Un=U0*M

Voila merci de m'aider.

Bonjour,

As-tu bien lu la réponse de Ben ? Je crois qu'on peut difficilement t'aider plus que ça pour cette propriété qui revient juste à "reconnaître" un produit matriciel. Il t'a même donné le détail de la formule.

Damien

[Alicia26]

Bonjour,

As-tu bien lu la réponse de Ben ? Je crois qu'on peut difficilement t'aider plus que ça pour cette propriété qui revient juste à "reconnaître" un produit matriciel. Il t'a même donné le détail de la formule.

Damien

Oui merci je viens de finir de la rédiger, je pensais qu'il y avait plus compliqué