Dans le cas où tu cherche par le calcul l'intersection d'une sphère et d'un plan et où les deux se coupent effectivement suivant un cercle (ce qui n'est pas le cas ici : ils sont tangents donc se coupent uniquement en un point), il n'est pas étonnant que tu ait l'impression de "tourner en rond", c'est à dire que tu n'arrive qu'à obtenir des équations de sphère :
La seule façon simple de définir un cercle dans l'espace de dimension 3, c'est de dire que c'est l'intersection d'un plan et d'une sphère ou bien de dire que c'est l'intersection de deux sphères...
A la limite, le seul truc un peu plus "visuel" auquel tu peut essayer d'arriver, c'est d'avoir une équation de plan et une équation de sphère dont le centre est dans le plan en question (en particulier, ça te permet de trouver le centre du cercle et son rayon...)
Ici, par exemple, tu as l'équation du plan : x+y+z=3 et l'équation
d'une des sphères définissant ton cercle (la sphère de centre (0,0,0) et de rayon

).
Pour trouver les autres sphères, tu fait l'équation de la sphère moins
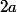
fois l'équation du plan :
+(y^2-2ay)+(z^2-2az)=3-6a)
Et tu met les trinômes sous "forme canonique" (i.e. tu fait apparaitre des identités remarquables)
+(y^2-2ay+a^2)+(z^2-2az+a^2)=3-6a+3a^2)
c'est à dire
^2+(y-a)^2+(z-a)^2=3a^2-6a+3)
Qui est l'équation de la sphère de centre (a,a,a) et de rayon

à condition que

.
Donc il faut chercher le minimum de

: s'il est 0, c'est le carré du rayon du cercle.
Ici, c'est "spécial" : comme
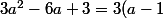^2)
le rayon va être nul pour a=1 donc la sphère va être réduite au point (a,a,a)=(1,1,1).
Enfin, une fois que tu as constaté ce fait, tu peut "tricher" en disant que, pour résoudre ton système, il suffisait de faire l'équation de la sphère - 2 x l'équation du plan et qu'on tombait en 2 lignes sur (x-1)²+(y-1)²+(z-1)²=0...
