Loi d'une variable aléatoire (géometrique et dite de Pascal)
17 messages
- Page 1 sur 1
Loi d'une variable aléatoire (géometrique et dite de Pascal)
Bonjour,
Je suis en L2 en AES et je vous serai très reconnaissant si je pouvais avoir un avis extérieur sur deux exercices de probabilité où je ne suis pas sur de mes résultats, voici lénoncé :
Un revolver à six coups ne contient quune balle dans son barillet que lon fait tourner de façon aveugle avant chaque tentative de tir. X est la variable aléatoire qui décrit lévénement "le coup part au Xème essai". Expliciter la loi de X (dite géométrique).
Variante collective du jeu (dite de l"ordre du Temple Solaire") : supposons que plusieurs personnes jouent successivement à ce jeu (dès quun joueur a gagné, il recharge le revolver et le passe au suivant).
Vous jouez en kème position et on désigne par Xk la variable aléatoire décrivant lévénement
G : "votre coup part à la Xk ème utilisation (collective) du revolver".
Expliciter la loi de Xk (dite de Pascal).
Préciser de plus votre temps dattente moyen avant lévénement G.
Pour ce faire, commencez par traiter les cas k= 2 et k= 3 avant de généraliser.
Voici mes résultats :
1) X représente le nombres de coup à effectuer pour arriver au 1er succès si on procède à des répétitions d'épreuves de Bernouilli, cad indépendantes entre elle.
X appartient ( 1,2,3...) = N ; k appartient à N ; p succès ; q = 1 - p échec ;
Donc p = 1/6 et q = 5/6
p(k) = 5/6^k-1. 1/6
Est-ce que c'est suffisant pour expliciter cette loi de variable aléatoire géométrique ?
2) Xk représente le nombre de coup à effectuer pour arriver au 1er succès si on procède à des répétitions collectives et indépendantes d'épreuve.
n = nombre de succès attendus ; p = probabilité d'un succès ; k appartient à N
f (k;n;p) = ( k + n -1 / k ) . p^n . q^k
Pour k = 2, n appartient à (1;2), un succès obligatoire car k=2 donc 2ème position
f (2;1;1/6) = (2+1-1 / 2) . 1/6 . 5/6²
f (2;2;1/6) = (2+2-1 / 2) . 1/6² . 5/6²
Pour k = 3, n appartient à (1;2;3)
f(3:1:1/6) = (3+1-1 / 3) . 1/6 . 5/6^3
f(3;2;1/6) = (3+2-1 / 3) . 1/6² . 5/6^3
f(3;3;1/6) = (3+3-1 / 3) . 1/6^3 . 5/6^3
A partir de là je suis perdu, ces cas aurai du m'aider à établir un cas général mais je vois vraiment pas comment...
Et je ne vois pas non plus le rapport avec le temps d'attente, qui me semble tout bonnement impossible à calculer car relatif au temps que les joueurs mettent pour effectuer leur tir.
Voilà, si vous avez des conseils ou des réponses à me donner je suis preneur, merci d'avance ! :lol3:
Je suis en L2 en AES et je vous serai très reconnaissant si je pouvais avoir un avis extérieur sur deux exercices de probabilité où je ne suis pas sur de mes résultats, voici lénoncé :
Un revolver à six coups ne contient quune balle dans son barillet que lon fait tourner de façon aveugle avant chaque tentative de tir. X est la variable aléatoire qui décrit lévénement "le coup part au Xème essai". Expliciter la loi de X (dite géométrique).
Variante collective du jeu (dite de l"ordre du Temple Solaire") : supposons que plusieurs personnes jouent successivement à ce jeu (dès quun joueur a gagné, il recharge le revolver et le passe au suivant).
Vous jouez en kème position et on désigne par Xk la variable aléatoire décrivant lévénement
G : "votre coup part à la Xk ème utilisation (collective) du revolver".
Expliciter la loi de Xk (dite de Pascal).
Préciser de plus votre temps dattente moyen avant lévénement G.
Pour ce faire, commencez par traiter les cas k= 2 et k= 3 avant de généraliser.
Voici mes résultats :
1) X représente le nombres de coup à effectuer pour arriver au 1er succès si on procède à des répétitions d'épreuves de Bernouilli, cad indépendantes entre elle.
X appartient ( 1,2,3...) = N ; k appartient à N ; p succès ; q = 1 - p échec ;
Donc p = 1/6 et q = 5/6
p(k) = 5/6^k-1. 1/6
Est-ce que c'est suffisant pour expliciter cette loi de variable aléatoire géométrique ?
2) Xk représente le nombre de coup à effectuer pour arriver au 1er succès si on procède à des répétitions collectives et indépendantes d'épreuve.
n = nombre de succès attendus ; p = probabilité d'un succès ; k appartient à N
f (k;n;p) = ( k + n -1 / k ) . p^n . q^k
Pour k = 2, n appartient à (1;2), un succès obligatoire car k=2 donc 2ème position
f (2;1;1/6) = (2+1-1 / 2) . 1/6 . 5/6²
f (2;2;1/6) = (2+2-1 / 2) . 1/6² . 5/6²
Pour k = 3, n appartient à (1;2;3)
f(3:1:1/6) = (3+1-1 / 3) . 1/6 . 5/6^3
f(3;2;1/6) = (3+2-1 / 3) . 1/6² . 5/6^3
f(3;3;1/6) = (3+3-1 / 3) . 1/6^3 . 5/6^3
A partir de là je suis perdu, ces cas aurai du m'aider à établir un cas général mais je vois vraiment pas comment...
Et je ne vois pas non plus le rapport avec le temps d'attente, qui me semble tout bonnement impossible à calculer car relatif au temps que les joueurs mettent pour effectuer leur tir.
Voilà, si vous avez des conseils ou des réponses à me donner je suis preneur, merci d'avance ! :lol3:
Salut,
Pour le 1), ça me parrait bon, modulo que
- {1,23,...} (avec des accolades : c'est un ensemble et pas un n-uplet) c'est plutôt N* que N
- Pour la formule, j'aurai plutôt écrit p(X=k)=... et j'aurais expliqué d'où sort la formule (il faut k-1 échecs suivi d'un succés et comme les épreuves sont indépendantes, on fait le produit)
Pour le 2), j'ai beau avoir lu 3 fois l'énoncé et ton résultat, je comprend pas (faut dire aussi que dans ta répons, c'est comme au 1), tu sort une formule de "derrière les fagots" sans trop qu'on sache comment on la prouve...)
Et dans l'énoncé lui même, ça :
Vous jouez en kème position et on désigne par Xk la variable aléatoire décrivant lévénement
G : "votre coup part à la Xk ème utilisation (collective) du revolver".
tel quel, ça se mord complètement la queue (on désigne par Xk un truc qui... dépend de Xk...) et j'ai beau me creuser les méninge, je vois vraiment pas ce que ça pourrait vouloir dire.
Est ce que tu peut expliquer ce que représente Xk ?
Pour le 1), ça me parrait bon, modulo que
- {1,23,...} (avec des accolades : c'est un ensemble et pas un n-uplet) c'est plutôt N* que N
- Pour la formule, j'aurai plutôt écrit p(X=k)=... et j'aurais expliqué d'où sort la formule (il faut k-1 échecs suivi d'un succés et comme les épreuves sont indépendantes, on fait le produit)
Pour le 2), j'ai beau avoir lu 3 fois l'énoncé et ton résultat, je comprend pas (faut dire aussi que dans ta répons, c'est comme au 1), tu sort une formule de "derrière les fagots" sans trop qu'on sache comment on la prouve...)
Et dans l'énoncé lui même, ça :
Vous jouez en kème position et on désigne par Xk la variable aléatoire décrivant lévénement
G : "votre coup part à la Xk ème utilisation (collective) du revolver".
tel quel, ça se mord complètement la queue (on désigne par Xk un truc qui... dépend de Xk...) et j'ai beau me creuser les méninge, je vois vraiment pas ce que ça pourrait vouloir dire.
Est ce que tu peut expliquer ce que représente Xk ?
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Salut,
Désolé pour les accolades et le manque de détail dans le calcul, c'est parce que j'ai du mal à transcrire les formules avec le clavier.
La formule je la sors du cours, mais ça mintéresserai d'en savoir davantage sur la façon de l'obtenir. Pourquoi il faut k -1 échec ?
Pour le 2) j'ai eu la formule du cours aussi, et vus que j'ai eu du mal à transcrire les signes ça peut porter à confusion.
Je peux t'envoyer lénoncé directement si ça peut t'aider à y voir plus clair !
Pour Xk c'est la variable aléatoire qui décrit l'événement G : succès après n utilisations collective.
Désolé pour les accolades et le manque de détail dans le calcul, c'est parce que j'ai du mal à transcrire les formules avec le clavier.
La formule je la sors du cours, mais ça mintéresserai d'en savoir davantage sur la façon de l'obtenir. Pourquoi il faut k -1 échec ?
Pour le 2) j'ai eu la formule du cours aussi, et vus que j'ai eu du mal à transcrire les signes ça peut porter à confusion.
Je peux t'envoyer lénoncé directement si ça peut t'aider à y voir plus clair !
Pour Xk c'est la variable aléatoire qui décrit l'événement G : succès après n utilisations collective.
Concernant la loi géométrique, ben c'est totalement évident : pour que la première fois qu'on réussi ça soit à la k-ième tentative, ben c'est forcément qu'on a fait k-1 echecs (de proba q) au début puis un succés (de proba p) ensuite.
Et concernant le 4), je capte toujours pas :
la variable aléatoire qui décrit l'événement G : succès après n utilisations collective.
Il me semble qu'une variable aléatoire dans des exos de ce type, c'est une valeur alors que là, "succès après n utilisations collective", c'est pas une valeur, c'est un truc qui est vrai ou qui est faux...
Et concernant le 4), je capte toujours pas :
la variable aléatoire qui décrit l'événement G : succès après n utilisations collective.
Il me semble qu'une variable aléatoire dans des exos de ce type, c'est une valeur alors que là, "succès après n utilisations collective", c'est pas une valeur, c'est un truc qui est vrai ou qui est faux...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Bon, je viens d'aller chercher sur wiki ce que pouvait bien être la "loi de Pascal" (ou binomiale négative selon wiki) : ça correspond au nombre d'échec que l'on a avant d'obtenir au total un nombre n fixé de succés (en faisant une série de tirages indépendants et de même proba)
A froid, je vois pas trop le rapport avec ton énoncé et ces différents joueurs...
A froid, je vois pas trop le rapport avec ton énoncé et ces différents joueurs...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
En fait lévénement G c'est lorsque le coup part (succès) après une succession d'échec et de succès faite par les joueurs d'avant.
Pour passer à un autre joueur il faut forcément un succès, donc on déduit qu'il y autant de succès que de position dans le jeux -1 : n = kème position -1 avec une probabilité de p=1/6
k représente le nombre d'échec et la position avec un probabilité de q = 5/6
En fait c'est la même chose que l'autre loi sauf que plutôt d'atteindre un succès, on en a autant que de joueurs.
Je crois voir le rapport avec l'énoncé, en gros le nombre d'échec nous indiquerai le temps moyen passé à attendre ?
Pour passer à un autre joueur il faut forcément un succès, donc on déduit qu'il y autant de succès que de position dans le jeux -1 : n = kème position -1 avec une probabilité de p=1/6
k représente le nombre d'échec et la position avec un probabilité de q = 5/6
En fait c'est la même chose que l'autre loi sauf que plutôt d'atteindre un succès, on en a autant que de joueurs.
Je crois voir le rapport avec l'énoncé, en gros le nombre d'échec nous indiquerai le temps moyen passé à attendre ?
Conclusion : comme tu est le k-ième joueur, ton "coup gagnant" à toi, ça sera le k-ième "coup gagnant" du flingue et la v.a.r. qu'on te demande d'étudier, c'est le nombre total de coups tirés avec le flingue avant ce k-ième succés.
Donc, clairement, X ne prend que des valeurs >= à k (le k-ième succés ne peut pas avoir lieu avant le k-ième essai...)
Bon, aprés, pour un n>=k donné, la proba que X soit égale à n, c'est la somme des proba de tout les successions d'essais (echec/réussite) tels que le n-ième tirage soit en fait la k-ième réussite.
Par exemple p(X=k)=p^k (pour que la k-ième réussite ait lieu au k-ième essai, ben il faut k réussites d'affilé)
Autre exemple (pour mieux comprendre) : si n=6 et k=3, ça veut dire que la 3 em réussite à lieu au 6em tirage : les séries possibles sont (E=Echec, R=réussite) :
RREEER ; REREER ; REERER ; REEERR ; ERREER ; ERERER ; EREERR ; etc...
Si on retourne au cas général, il faut clairement qu'on ait une "série" de n tirages avec k réussite et n-k échecs.
Une fois l'ordre des réussites/echecs fixés, la proba d'une telle série est donc de^{n-k})
Et il suffit donc de regarder combien il y a de "telles" séries.
Le dernier coup doit être une réussite et, sur les n-1 précédents, il doit y avoir k-1 réussite donc le nombre de séries possible est (coeff. binomial)
(coeff. binomial)
Bilan :={n-1 \choose k-1} p^k(1-p)^{n-k}) (pour
(pour 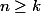 )
)
et ce n'est pas exactement la "loi de pascal" qui elle ne compte que le nombre d'échecs avant la k-ième réussite et pas le nombre de coup total.
Donc, clairement, X ne prend que des valeurs >= à k (le k-ième succés ne peut pas avoir lieu avant le k-ième essai...)
Bon, aprés, pour un n>=k donné, la proba que X soit égale à n, c'est la somme des proba de tout les successions d'essais (echec/réussite) tels que le n-ième tirage soit en fait la k-ième réussite.
Par exemple p(X=k)=p^k (pour que la k-ième réussite ait lieu au k-ième essai, ben il faut k réussites d'affilé)
Autre exemple (pour mieux comprendre) : si n=6 et k=3, ça veut dire que la 3 em réussite à lieu au 6em tirage : les séries possibles sont (E=Echec, R=réussite) :
RREEER ; REREER ; REERER ; REEERR ; ERREER ; ERERER ; EREERR ; etc...
Si on retourne au cas général, il faut clairement qu'on ait une "série" de n tirages avec k réussite et n-k échecs.
Une fois l'ordre des réussites/echecs fixés, la proba d'une telle série est donc de
Et il suffit donc de regarder combien il y a de "telles" séries.
Le dernier coup doit être une réussite et, sur les n-1 précédents, il doit y avoir k-1 réussite donc le nombre de séries possible est
Bilan :
et ce n'est pas exactement la "loi de pascal" qui elle ne compte que le nombre d'échecs avant la k-ième réussite et pas le nombre de coup total.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Si j'ai bien compris n correspond au nombre de tirage et k est juste un entier naturel non nul ?
Par contre comment tu fixe l'ordre des réussites/échecs ?
Je comprend comment tu obtiens la formule du cas général, mais comment avec k=2 et k=3 j'étais censé la trouver ?
Avec cette formule je peux calculer le nombre de coup moyen effectuer avant le k ième coup gagnant au n ième dernier tirage, quel rapport avec le temps d'attente ?
Je te remercie beaucoup pour ces premières informations, ça m'a bien fait cogiter mais j'ai encore pas mal de zone de floue. Faut dire que j'ai du mal à comprendre les maths seulement en lisant.
Par contre comment tu fixe l'ordre des réussites/échecs ?
Je comprend comment tu obtiens la formule du cas général, mais comment avec k=2 et k=3 j'étais censé la trouver ?
Avec cette formule je peux calculer le nombre de coup moyen effectuer avant le k ième coup gagnant au n ième dernier tirage, quel rapport avec le temps d'attente ?
Je te remercie beaucoup pour ces premières informations, ça m'a bien fait cogiter mais j'ai encore pas mal de zone de floue. Faut dire que j'ai du mal à comprendre les maths seulement en lisant.
Sarp25 a écrit:Pourquoi n-k échecs pour le cas général ? Pour toi k est indifférent de l'échec ou la réussite et c'est juste le nombre total de coup tiré ?
Comment tu fixe l'ordre des réussites/échecs ?
Est-ce que tu peux écrire exactement ce que représente n et k pour toi ?
Quitte à utiliser d'autres lettres parce que je suis encore plus paumé qu'avant.
k il est complètement totalement "fixé" : c'est absolument partout le même et il correspond à la position que tu as dans le fameux jeu (1er ou 2em ou 3em... et tu change pas de place en cours de jeu). Comme tu joue k-ième, dans la série complète des "coups" du flingue, lorsque toi tu va réussir, ça sera la k-ième réussite du flingue.
n lui, il est un peu moins fixé (c'est pour ça qu'on intéresse à la proba que X=n...), c'est à dire qu'on le fixe le temps de calculer cette fameuse proba mais qu'aprés dans l'exo, il y a de forte chance qu'on s'intéresse à des valeurs différentes de n.
Il correspond au nombre total d'utilisation du flingue pour arriver jusqu'à TA réussite à toi (qui sera donc la k-ième réussite pour le flingue)
Reregarde l'exemple k=3 et n=6. Si par exemple la série est REERER, ça veut dire que le premier joueur à réussi du premier coup (en vert) puis a passé le flingue au deuxième joueur qui a echoué 2 fois et réussi au 3em essai (en rouge) et qui t'a filé le flingue (k=3 -> tu es le 3em joueur) tu as échoué au premier essai et réussi au deuxième (en bleu)
Au total, TA réussite A TOI, elle a eu lieu à la 6em utilisation du flingue donc on est dans UN DES CAS où n=6.
Pour avoir la proba que X=6, ben il faut regarder TOUT les cas conduisant à ce même résultat de n=6.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Sarp25 a écrit:Les différentes séries possible ça j'ai compris, mais comment tu fixes l'ordre des réussites/échec pour établir un cas général ? Parce que comme tu l'as écris, il faut regarder tout les cas conduisant à ce même résultat, alors comment tu choisis le bon ?
Y'a pas de "bon" ou de "mauvais" cas : il faut tous les énumérer pour pouvoir dire que la proba que ta réussite arrive en n-ième position, ben c'est la somme des proba de tout les cas qui donnent la k-ième réussite en n-ième position.
Heureusement chaque cas à la même proba, à savoir
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Après pas mal de tentative je crois avoir compris le raisonnement.
Si bien que la question du temps d'attente moyen me semble de plus en plus absurde !
Je sais qu'il sera dépendant de k, et plus k sera grand plus le temps d'attente sera long, mais de là à établir un temps d'attente moyen...
A moins qu'on ne doit calculer ce temps que pour k=2 ou k=3 mais là encore il faudrait que je fixe un "temps" pour chaque essaie, ce qui me semble être plus du bidouillage que des mathématiques.
Merci de ta patience et de tes réponses, tu m'as beaucoup aidée jusquà présent ! :)
Si bien que la question du temps d'attente moyen me semble de plus en plus absurde !
Je sais qu'il sera dépendant de k, et plus k sera grand plus le temps d'attente sera long, mais de là à établir un temps d'attente moyen...
A moins qu'on ne doit calculer ce temps que pour k=2 ou k=3 mais là encore il faudrait que je fixe un "temps" pour chaque essaie, ce qui me semble être plus du bidouillage que des mathématiques.
Merci de ta patience et de tes réponses, tu m'as beaucoup aidée jusquà présent ! :)
Le "temps d'attente moyen", c'est ce qu'on apelle en math "l'espérance" d'une variable aléatoire et ça correspond à faire la somme des pi.Xi où les xi représentent les différentes valeur que prend la variable aléatoire et les pi les proba correspondantes.
Par exemple, pour un dés à 6 façe usuel, les résultats possibles sont 1,2,3,4,5,6 avec des probas de 1/6 à chaque fois. L'espérance est donc (1/6).1+(1/6).2+(1/6).3+(1/6).4+(1/6).5+(1/6).6 = 3,5.
Dans ton exo, il y a une infinité de résultat possibles (tout les entiers supérieurs ou égaux à k) donc ça te fait une somme infinie :
\ =\ \sum_{n\geq k}p(X=n)\times n\ =\ \sum_{n\geq k}{n-1 \choose k-1}p^k(1-p)^{n-k}\times n=...=\frac{k}{p})
Par exemple, pour un dés à 6 façe usuel, les résultats possibles sont 1,2,3,4,5,6 avec des probas de 1/6 à chaque fois. L'espérance est donc (1/6).1+(1/6).2+(1/6).3+(1/6).4+(1/6).5+(1/6).6 = 3,5.
Dans ton exo, il y a une infinité de résultat possibles (tout les entiers supérieurs ou égaux à k) donc ça te fait une somme infinie :
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
17 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 91 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
