Salut,
J'aimerais revenir sur cet exo et montrer que la "log-vraisemblance" (c'est-à-dire la fonction
))
) est une fonction
strictement concave.
J'ai calculé cette log-vraisemblance ainsi que les dérivées partielles premières et secondes par rapport à

.
Tout d'abord, si je note
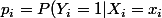)
alors on obtient
(*) =\sum_{i=1}^{n}y_i ln(p_i) + \sum_{i=1}^{n} (1-y_i)ln(1-p_i))
 = \sum_{i=1}^{n} \left[y_i \theta x_i - ln \left(1+e^{\theta x_i}\right) \right])
}{\partial \theta} = \sum_{i=1}^{n} \left[ y_i x_i - \frac{x_{i}e^{\theta x_i}}{1+e^{\theta x_i}}\right])
}{\partial \theta^{2}} = - \sum_{i=1}^{n} \frac{x_{i}^{2}e^{\theta x_i}}{\left(1+e^{\theta x_i}\right)^2})
En analysant l'expression de la dérivée seconde, on remarque qu'elle est strictement négative pour xi != 0 et nulle si xi=0.
En gros l'expression est négative définie. Donc il existe un unique maximum local pour la vraisemblance qui est aussi celui de la log-vraisemblance puisque la fonction log est croissante (strictement) et la vraisemblance positive. Autrement-dit, la fonction log-vraisemblance est strictement concave.
Est-ce que c'est correct ou pas ?? ...
De toute façon, d'après
(*), on obtient une fonction qui est somme de deux fonctions concaves (puisque le log est concave), elle est donc concave.
Je n'ai pas eu de cours sur ce sujet, mais je m'entraine et regarde la doc sur internet quoi.
Merci
