Maximum vraisemblance

[Raven]

Bonjour ,

J'ai un exercice d'estimation ponctuelle , le voici :
http://www.hostingpics.net/viewer.php?id=526730IMAGE2.jpg

1) pour la question 1 , j'ai trouvé comme estimateur â : n/Somme des (Ln(1+xi)^c)

2)Je n'arrive pas à trouver la fonction de répartition , car je n'arrive pas à intégrer sur [0,a] la densité , fin trouver une primitive ...

[DamX]

Bonjour,

1) oui, sauf que le ^c est mal placé mais je suppose que c'est une erreur de recopie

2) quelle est la dérivée (en x bien sur) de [1+x^c]^(-a) ?

Damien

[Raven]

C'est n/Somme des Ln(1+xi)^c ?

2) f'(x)= -a(1x^c)^(-a-1)*cx ?

[DamX]

C'est n/Somme des Ln(1+xi)^c ?

Euh tu as recopié la Meme chose là... c'est juste que le "puissance c" porte sur le Xi uniquement
Ca fait n / Somme[ ln(1+Xi^c) ]

2) f'(x)= -a(1x^c)^(-a-1)*cx ?

Pas exactement non...
C'est -ac x^(c-1) [1+x^c]^(-a-1), ce qui ressemble très fortement à.. ?

[Raven]

ah oui oui j'avais pas tenu comme de x^c...
Sinon ça ressemble à fa(x)?

[DamX]

ah oui oui j'avais pas tenu comme de x^c...
Sinon ça ressemble à fa(x)?

C'est Meme égal à -fa(x)

[Raven]

Du coup la Fa(x)= -(1+x^c)^(-a)Indicatrice de x>0
Et pour la fonction quantile , le paramètre à isoler là c'est x ?

[DamX]

Du coup la Fa(x)= -(1+x^c)^(-a)Indicatrice de x>0
Et pour la fonction quantile , le paramètre à isoler là c'est x ?

Le fait que Fa(x) telle que tu l'as écrite soit négative ne te choque pas pour une fonction de répartition ?

[Raven]

donc c'est égal à fa(x)?

[DamX]

donc c'est égal à fa(x)?

non plus..

Quand tu intègres quelque chose entre 0 et x le résultat c'est la primitive prise en x - la primitive prise en 0.

[Raven]

ah ok oui merci

[alegaxandra]

Du coup la Fa(x)= -(1+x^c)^(-a)Indicatrice de x>0
Et pour la fonction quantile , le paramètre à isoler là c'est x ?

Regardez à: [url=fr.wikipedia.org/wiki/Liste_des_lois_de_probabilité]La liste des lois de probabilité.[/url] On a donc la fonction de répartition qui signifie la probabilité :


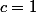
Si , la loi de Burr devient la loi de Pareto.