Vecteur binaire

[jankyjack]

bonsoir,

j'ai eu à faire ce dernier temps au vecteur binaire et j'aimerai savoir ce que c'est.
e si possible quelques illustrations.

je vous remercie pour vos réponses

[fatal_error]

je connais pas cette notation mais je presume que cest un vecteur de taille n composé que de zeros ou de uns.

pour les illus tu as par ex http://stackoverflow.com/questions/1236 ... ted-graphs

ou tu utilises un vecteur binaire pour representer un cycle dans un graphe

[jankyjack]

cette notation en fait represente le produit cartésien et ce sont les elements issus de ce produit cartésien que je considére comme un vecteur binaire.

merci pour la doc mais je l'ai parcouru et je ne vois pas suffisament de détails sur les vecteurs binaires. ils en parlent mais brièvement. du genre ce que j'ai rencontré avant de venir ici pour poser ma question.

[Ben314]

Salut,

cette notation en fait represente le produit cartésien et ce sont les elements issus de ce produit cartésien que je considére comme un vecteur binaire.

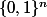
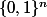
Déjà, si c'est les éléments de l'ensemble qui sont des "vecteurs", c'est on ne peu plus con d'écrire "le vecteur ". Pour toi, un sac de bonbons c'est un bonbon ou pas ? Là, c'est pareil.
(et à mon avis c'est pour ça que fatal n'a pas compris de quoi tu parlait vu qu'on imagine difficilement quelqu'un confondre un contenant avec son contenu)

Et si on regarde les éléments de {0,1}^n comme des vecteurs, c'est qu'on peut munir l'ensemble {0,1} d'opérations (+ et x) comme dans R et qu'ensuite, les additions sur les éléments de {0,1}^n vont se faire "terme à terme" comme sur les éléments de R^n qui représentes eux, les vecteurs usuels : tu as surement déjà manipulé le "vecteur (x,y)" de R^2.

Bref, les ensembles de ce type là, ça s'appelle des "espaces vectoriels" et les éléments de tels espaces sont appelés des "vecteurs".

[jankyjack]

je n'ai rien confondu. c'est juste un manque de point virugule dans l'enoncé du problème. je voulais dire que j'ai eu à faire aux vecteurs binaires. puis je fais juste une petite précision pour que vous ayez deja aumoíns une petite référence de quoi je parle et c'est dans cette optique que j'ai précisé {0,1}^n