Valeurs d'adhérence

[egan]

Salut tout le monde,

A l'époque où j'ai vu les valeurs d'adhérence, on ne considérait que les valeurs d'adhérence réelles. C'est un peu restrictif pour attaquer les lim inf et les lim sup. Du coup, je veux m'intéresser aux valeurs d'adhérence dans .

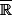
Je sais que:
- toute suite bornée admet au moins une valeur d'adhérence réelle.
- une suite bornée converge si et seulement si elle n'a qu'une seule valeur d'adhérence réelle.

J'aimerais étendre tout ça aux valeurs d'adhérence dans .

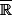
Est-ce qu'il est vrai que:

- toute suite réelle admet au moins une valeur d'adhérence dans .
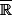
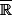
- toute suite réelle converge dans si et seulement si elle n'a qu'une seule valeur d'adhérence dans .

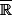
Merci d'avance.
@+ Boris.

[leon1789]

Est-ce qu'il est vrai que:

- toute suite réelle admet au moins une valeur d'adhérence dans .
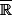
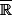
- toute suite réelle converge dans si et seulement si elle n'a qu'une seule valeur d'adhérence dans .

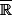
pense justement aux limite_inf et limite_sup

[egan]

Je suis en train de m'approprier les lim inf et les lim sup. J'aimerais bien des réponses qui n'y font pas appel. ^^

Je voudrais en fait me servir de ces résultats pour lesquels je veux confirmation pour montrer certains trucs sur les lim inf et les lim sup.

[egan]

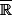
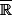
Pour les lim sup et les lim inf, je dois montrer que la lim inf est la plus petite valeur d'adhérence dans et que la lim sup est la plus grand valeur d'adhérence dans . En particulier ça permettrait de montrer que toute suite admet une valeur d'adhérence dans .

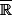
Je bloquais justement sur cette démo. Comment montrer que la lim sup est une valeur d'adhérence et comment montrer que c'est la plus grande ?

[leon1789]

Ce que tu dis est correct, et tes questions sont normales.

La limite_sup est une valeur d'adhérence : montrer l'existence d'une sous-suite qui tend vers limite_sup.

La limite_sup est supérieure ou égale à toute valeur d'adhérence : reprendre les définitions de limite_sup et de valeur d'adhérence.

Je suis assez peu précis pour que tu puisses, comme tu l'as fait jusqu'à maintenant, y réfléchir tranquillement.

[egan]

Comment sont définies les valeurs d'adhérence dans ?

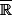
Pour les valeurs d'adhérence dans , on a toujours les trois définitions suivantes qui sont équivalentes:

- a est une valeur d'adhérence réelle si et seulement si elle est limite d'une suite extraite.
- a est une valeur d'adhérence réelle si et seulement si , l'ensemble
- a est une valeur d'adhérence infinie si et seulement si pour tout A>0, l'ensemble est infini.

Je viens aussi de me rendre compte qu'il ne doit pas être trop faux de remplacer les inégalités strictes dans ces conditions par des inégalités larges.

[leon1789]

Comment ça se passe si la valeur d'adhérence est infinie ? On a toujours la définition:

- a est une valeur d'adhérence infinie si et seulement si elle est limite d'une suite extraite.

Existe-t-il d'autres caractérisations un peu comme celles aves les valeurs d'adhérence finies ?

Je sens bien le truc du genre:

- +infini est une valeur d'adhérence si et seulement si
- +infini est une valeur d'adhérence si et seulement si pour tout A>0, l'ensemble est infini.

:++:

Continue, tu comprends bien.

Je viens aussi de me rendre compte qu'il ne doit pas être trop faux de remplacer les inégalités strictes dans ces conditions par des inégalités larges.

exact.

(pour les limites finies, il faut toujours prendre )

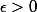
[egan]

Ce que tu dis est correct, et tes questions sont normales.

La limite_sup est une valeur d'adhérence : montrer l'existence d'une sous-suite qui tend vers limite_sup.

La limite_sup est supérieure ou égale à toute valeur d'adhérence : reprendre les définitions de limite_sup et de valeur d'adhérence.

Je suis assez peu précis pour que tu puisses, comme tu l'as fait jusqu'à maintenant, y réfléchir tranquillement.

J'ai réussi à montrer que la limite sup était une valeur d'adhérence quand celle-ci est égale à +oo mais je n'y arrive pas quand elle est finie. Je n'arrive pas à construire la sous-suite. Est-ce que tu peux me donner une indication stp ?
Je voulais passer par la caractérisation "pour tout epsilon strictement positif, l'ensemble ... est infini" mais je bloque.

[egan]

Personne ?

[Le_chat]

Je sais pas si ça te simplifie la tâche mais tu peux remplacer "pour tout epsilon strictement positif, l'ensemble ... est infini" par "pour tout epsilon strictement positif, l'ensemble ... est non vide", sauf erreur...

[egan]

Ca doit pouvoir passer avec ça mais je ne vois pas pourquoi ces deux conditions seraient équivalentes.

[Le_chat]

Si ".. est infini" alors "... est non vide".

Dans l'autre sens, si pour tout A reel, "... est non vide", soit B un réel, supposons par l'absurde que la partie {n, tel que un>B} soit non infinie i.e. finie (et non vide par hypothèse). On prend alors n' dans cette partie tel que u_n' soit maximal. Ben alors {n, tel que un>un'} est vide, ce qui est faux par hypothèse.


On peut aussi montrer directement que si la partie "..." est non vide pour tout reel, la suite admet l'infini comme v.a., en construisant une extraction à la main.

[egan]

Merci pour ta réponse !

[egan]

Je voulais en fait montrer ce résultat pour une valeur d'adhérence finie mais je ne vois pas comment adapter la preuve que tu proposes. Au lieu de m'intéresser au max, je prends plutôt le min mais rien me garantie qu'il sera strictement positif.
Tu vois comment contourner le problème ?