Urgent j'ai besoin d'aide! Merci!

[Nickzalktov]

trouver tous les polynôme de degré 4 tel que p(x^2)=p(x)p(x-1)


Je suis sur la piste ax^4+bx^3+cx^2+dx+e mais je n'obtiens pas de réponse considérable!
Je vais devenir fou!

Merci d'avance =)

[Nightmare]

Salut,

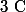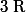Tu n'as pas précisé dans quel corps on travaille, mais je suppose que c'est ou . Sur 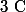, on a l'existence d'au moins une racine complexe a de P.

On remarque alors que P(a²)=P(a)P(a-1)=0, de même P(a^4)=P(a^8)=...=0 et comme un polynôme n'a qu'un nombre fini de racine, ceci exige que a=0 ou que |a|=1. De même (a+1)², (a+1)^4 etc... sont des racines, donc |a+1|=1 ou a=1 ce qui implique que les seules racines possibles sont 0, 1, j et j².

A toi de conclure.

[Nickzalktov]

Donc déjà j'ai oublier de préciser comme tu l'a fait remarquer je travail dans R
De plus j'ai pratiqué par identification mais je bloque!
Car en fin de compte je trouve des résultats incohérents au degré 3 lorsque japplique une vérification!

[Nightmare]

L'identification ne me semble pas être la méthode la plus simple, étant donné les calculs à fournir, c'est pour cela que je t'ai proposé une alternative, en raisonnant sur l'identité qu'on te donne.

[Nickzalktov]

C'est pas bizarre qu'il n'y est qu'une solution alors que l'enoncé demande toute les solutions?
Développe un peu stp je suis juste en bac +1!!

[Nightmare]

De quelle(s) solution(s) parles-tu ?

La solution est bien de niveau bac+1, le seul théorème "fort" que j'utilise, c'est le fait qu'un polynôme complexe non constant a au moins toujours une racine complexe.

[arnaud32]

bonjour,

en effet tu peux constater que l'ensemble des racines de P est stable par x->x² et x->(x+1)²
cependant P possede au plus 4 racines.
Si tu as une racine r, r² est racine.
si r=r², alors r=1 ou r=0
dans le cas r=1 on a (r+1)²=2²=4 qui est racine et 5²=25 qui l'st aussi etc. donc tu as une infinite de racines, ce qui est impossible pour un polynome de degre 4.
dans le cas r=0 on a (r+1)²=1 qui est racine et tu te ramene au cas precedent.

tu en conclus que r et r² sont toujours distincts.

r² etant racine (r²)² est racine aussi, comme tu ne peux pas avoir r²=(r²)² tu as une autre racine sauf si r^4=r.
or tu sais que r est different de 0 et 1; r est donc j ou j² les deux autres racine cubiques de l'unite.
(j+1)² = j²+2j+1=j car j²+j+1 = 0 (relation de la somme des racines d'un polynome)
(j²+1)² = j^4+2j²+1 = j+2j²+1 = j²
tu as donc un sous ensemble de l'ensemble des racines qui est stable par les deux fonctions du depart.

on a donc trois racines distinctes r, r², r^4 ou le couple (j,j²) (avec des multiplicites possibles)

si r^8 est distinct de r, r², r^4 on a les 4 racines de P et il faut verifier que {r,r^2,r^4,r^8} est stable par les deux fonctions, ce qui doit te restrindre les cas possibles.

Sinon tu dois etudier r^8=r ou r^8=r² ( excluant comme racines, 0, 1 et meme -1 car -(1+1)²=0 impliquerais que zero soit racine.

ps: j'essaierais de t'aider a finir plus tard

[arnaud32]

Excuses moi, j'ai un peu divague.
En combinant la reponse de Nightmare et la mienne, tu trouves que les seules racines possibles sont j et j² et qu'elles doivent etre toutes les deux racines.
tu as donc
(x-j) * (x-j²)^3
(x-j)² * (x-j²)²
(x-j)^3 * (x-j²)

si tu dois travailler dans R, il faut que tu regardes s'ils sont a coefficients reels ou non.

[Nickzalktov]

tu aurais moyen de detailler stp
on a planché dessus durant la soirée avec les collegues mais on trouve pas :S

[arnaud32]

je vais reprendre ce qui a ete ecrit precedement.

tu as pour tout x P(X²)=P(X)*P(X-1) P polynome de degre 4

P admet une racine complexe r.

P(r²)=P(r)*P(r-1)=0 car P(r)=0
donc r² est aussi une racine de P. Tu peux montrer par recurence que r^(2^k) est racine pour tout k entier naturel.
Tu as donc une suite de racines complexes de module |r|^(2^k).
Si |r|=0, r=0; sinon
Si |r|>0 est differtent de 1 la suite est strictement monotone (strictement croissante pour |r| > 1; strictement decroissante pour |r|<1) donc a une infinite de valeurs.
Cependant un polynome n'a qu'un nombre fini de racines (ce nombre est majore par son degre).
Ce qui est absurde.
On en conclu que |r|=1 ou r=0

P((r+1)²)=P(r+1)*P(r)=0 car P(r)=0
donc (r+1)² est aussi une racine, et son module vaut aussi 1: |r+1|²=|(r+1)²|=1 et |r+1|=1

si r=0, (r+1)²=1 est racine et (1+1)²=2² est aussi racine pareil pour (1+2²)² etc... on a donc une suite strictement croissante de racines, ce qui est en contradiction avec le fait que P est un polynome.
On a donc montre que 0 et 1 ne peuvent etre des racines de P.

il reste le systeme |r|=1 et |r+1|=1 qui se resoud dans le corps de complexe.
les solutiuons sont j et j² les racine cubique de l'unite autre que 1.
En effet on a:
|r+1|=1 et |r|=1 ssi (r+1)*(r'+1)=1 et r*r'=1 (r' conjugue de r)
ssi r*r'+(r+r')+1=1 et r*r'=1
ssi r+r'=-1 et r*r'=1
ssi r et r' racines de x²+x+1
on coclu grace a x^3-1 =(x-1)*(x²+x+1)
geometriquement, ce sont les points d'intersection des cercles de centre 0 et -1 et de rayon 1.

(j+1)² = j²+2j+1=j car j²+j+1 = 0 (relation de la somme des racines du polynome x^3-1)
(j²+1)² = j^4+2j²+1 = j+2j²+1 = j²

l'ensemble {j,j²} est donc bien stable par x -> x² et x -> (1+x)²

On a donc prouve que les seules racines possibles de P sont j et j². (et ce sans utiliser le degre de P)

P etant scinde sur C, P(x)=(x-a)(x-b)(x-c)(x-d) ou a,b,c,d sont dans {j,j²}