Unité approchée de convolution...
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
franz2b
- Membre Naturel
- Messages: 40
- Enregistré le: 10 Mai 2006, 15:04
-
 par franz2b » 05 Déc 2007, 22:15
par franz2b » 05 Déc 2007, 22:15
Salut tout le monde,
j'aimerai avoir une petite aide.
Soit la fonction
*K(t)=1 si 02 (ce sont des (inférieur et superieur ou égal))
------------------>La fonction K est donc une fonction plateau.
*Pour tout n naturel, on pose:
=K(x/n))
*On note enfin
)
la transformée de Fourier de K.
J'aimerai montrer que
)
est une unité approchée de convolution.
Je n'arrive ni à montrer que
||_1=1)
(En fait,
||_1=K_n(0)=1)
! Mais pourquoi?!)
Ni a montrer que
)\, \mathrm dx\to0)
pour
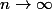
Merci a tous
-
franz2b
- Membre Naturel
- Messages: 40
- Enregistré le: 10 Mai 2006, 15:04
-
 par franz2b » 06 Déc 2007, 23:47
par franz2b » 06 Déc 2007, 23:47
J'ai rectifié l'enoncé......désolé.
j'espere avoir de vos aides tres bientot merci.
 par busard_des_roseaux » 07 Déc 2007, 00:20
par busard_des_roseaux » 07 Déc 2007, 00:20
bonsoir,
j'ai fait ça aujourd'hui entre 15 et 16 h !
d'après ma prof, les propriétés à vérifier sont:

 dt = 0)
-
franz2b
- Membre Naturel
- Messages: 40
- Enregistré le: 10 Mai 2006, 15:04
-
 par franz2b » 07 Déc 2007, 01:34
par franz2b » 07 Déc 2007, 01:34
busard_des_roseaux a écrit:bonsoir,
j'ai fait ça aujourd'hui entre 15 et 16 h !
d'après ma prof, les propriétés à vérifier sont:

 dt = 0)
lol
merci jeune homme, c'est effectivement bien ce qui est a demontrer, mais cela ne m'avance pas, car je ne sais pas le demontrer....peut etre pourrais tu m'aider?
merci

ps: il y a mm une troisieme propriété evidente mais importante: Kn >0
re ps: pour la limite de l'itegrale, il faut surement faire un changement de variable interessant pour faire tendre

-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 07 Déc 2007, 15:51
par tize » 07 Déc 2007, 15:51
Bonjour,
il me semble que pour ce genre de chose on montre que
)
est aussi intégrable (ici c'est le cas car
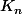
est

à support compact est dans l'espace de Schwartz donc sa transformée de Fourier est aussi dans l'espace de Schwartz). On a donc la formule d'inversion :
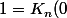=\frac{1}{2\pi}\int_{\mathbb{R}}F\(K_n\)(x)dx)
-
franz2b
- Membre Naturel
- Messages: 40
- Enregistré le: 10 Mai 2006, 15:04
-
 par franz2b » 07 Déc 2007, 16:19
par franz2b » 07 Déc 2007, 16:19
tize a écrit:Bonjour,
il me semble que pour ce genre de chose on montre que
)
est aussi intégrable (ici c'est le cas car
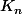
est

à support compact est dans l'espace de Schwartz donc sa transformée de Fourier est aussi dans l'espace de Schwartz). On a donc la formule d'inversion :
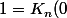=\frac{1}{2\pi}\int_{\mathbb{R}}F\(K_n\)(x)dx)
Merci infiniment Tize, j'avais oublié la bonne vieille formule
+f(x-)}{2}=\int f(x) e^{ikx}\,dx)
Ici appliquée en 0
Et pour ce qui est de
\,dx\rightarrow__{n \to \infty} 0)
comment faire?
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 07 Déc 2007, 16:46
par tize » 07 Déc 2007, 16:46
Je ne comprends plus, au début tu voulais montrer que
)\, \mathrm dx\to0)
pour
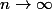
et maintenant tu veux montrer que c'est
\,dx\rightarrow__{n \to \infty} 0)
?
ou alors tu as oublié le F ?
-
franz2b
- Membre Naturel
- Messages: 40
- Enregistré le: 10 Mai 2006, 15:04
-
 par franz2b » 07 Déc 2007, 17:09
par franz2b » 07 Déc 2007, 17:09
tize a écrit:Je ne comprends plus, au début tu voulais montrer que
)\, \mathrm dx\to0)
pour
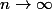
et maintenant tu veux montrer que c'est
\,dx\rightarrow__{n \to \infty} 0)
?
ou alors tu as oublié le F ?
oups!! au temps pour moi, j'ai bien fait l'oublie d'une transformée (d'un F)
je veux bien sure que:
(x)\,dx\rightarrow__{n \to \infty} 0)
Encore désolé
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 07 Déc 2007, 17:16
par tize » 07 Déc 2007, 17:16
Bon je vais supposer que c'est avec F (autrement ça me parait faux...)
(x)dx = \int_{|x|>\epsilon}\(\int_{\mathbb{R}}e^{-itx}K(t/n)dt\)dx)
ensuite utilise le fait que
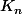
ainsi que ses dérivées sont nulles en dehors

et fait 2 IPP, pour obtenir quelque chose qui ressemble à :
dt\)dx)
on peut alors (sauf erreur de ma part) majorer en module tout ceux petit monde par une constante fois 1/n...
-
franz2b
- Membre Naturel
- Messages: 40
- Enregistré le: 10 Mai 2006, 15:04
-
 par franz2b » 07 Déc 2007, 17:48
par franz2b » 07 Déc 2007, 17:48
tize a écrit:Bon je vais supposer que c'est avec F (autrement ça me parait faux...)
(x)dx = \int_{|x|>\epsilon}\(\int_{\mathbb{R}}e^{-itx}K(t/n)dt\)dx)
ensuite utilise le fait que
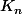
ainsi que ses dérivées sont nulles en dehors

et fait 2 IPP, pour obtenir quelque chose qui ressemble à :
dt\)dx)
on peut alors (sauf erreur de ma part) majorer en module tout ceux petit monde par une constante fois 1/n...
:++:
Merci beaucoup mec, je vais faire ca de mon coté, mais j'imagine que les IPP ne doivent pas poser trop de pb.
Combien j'te dois? :zen:
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 07 Déc 2007, 17:51
par tize » 07 Déc 2007, 17:51
franz2b a écrit:Combien j'te dois? :zen:
Un gros bisou sur la fesse droite...ciel ma femme est rentrée !

-
franz2b
- Membre Naturel
- Messages: 40
- Enregistré le: 10 Mai 2006, 15:04
-
 par franz2b » 07 Déc 2007, 17:57
par franz2b » 07 Déc 2007, 17:57
tize a écrit:Bon je vais supposer que c'est avec F (autrement ça me parait faux...)
(x)dx = \int_{|x|>\epsilon}\(\int_{\mathbb{R}}e^{-itx}K(t/n)dt\)dx)
ensuite utilise le fait que
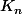
ainsi que ses dérivées sont nulles en dehors

et fait 2 IPP, pour obtenir quelque chose qui ressemble à :
dt\)dx)
on peut alors (sauf erreur de ma part) majorer en module tout ceux petit monde par une constante fois 1/n...
Bon j'ai fais mes IPP et j'arrive bien au resultat.
Cependant, comment justifies tu le fait que la derivée d'une fonction a decroissance rapide est une fonction a decroissance rapide?
(est ce vrai deja?)
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 07 Déc 2007, 18:02
par tize » 07 Déc 2007, 18:02
on en a pas besoin ici,
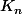
est nulle en dehors de [-2n;2n] donc toutes ses dérivées le sont aussi...elles sont donc bien intégrables...
-
franz2b
- Membre Naturel
- Messages: 40
- Enregistré le: 10 Mai 2006, 15:04
-
 par franz2b » 07 Déc 2007, 18:03
par franz2b » 07 Déc 2007, 18:03
j'ai rien dit, on integre pas sur moins l'infini , l'infini mais sur -2n 2n......et en ces valeurs si la fonction est nulle.....bah la derivée le sera deux fois plus :)
.....A+
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 36 invités
