Une question sur (Z/nZ)* please

par **RadarX** » 19 Aoû 2005, 10:24

L'ensemble (Z/nZ)* des elements inversibles de Z/nZ ( qui est aussi egal l'ensemble des classes k+nZ tel que k et n soient premiers entre eux) est un groupe multiplicatif d'ordre phi(n) (indicateur d'euler). Et il est meme cyclique.

Alors est-ce que quelqu'un peut m'en trouver un generateur, c'est a dire de (Z/nZ)*?

RadarX.

par **palmade** » 19 Aoû 2005, 20:48

Malgré le ton péremptoire de la demande,

(EDIT Alpha (modérateur) : le titre original de la discussion n'était pas le titre actuel)

il serait étonnant que tu obtiennes une réponse pour la bonne raison que le groupe multiplicatif des élements inversibles de Z/nZ n'est pas toujours cyclique!
Prend par exemple Z/15Z, Il y a bien phi(15)=8 éléments inversibles: (1,2,4,7,8,11,13,14) mais pas de cycle: outre 1, deux éléments 4 et 14 sont leurs propres inverses, ce qui est impossible dans un groupe cyclique!

par **RadarX** » 19 Aoû 2005, 22:22

palmade a écrit:Malgré le ton péremptoire de la demande, il serait étonnant que tu obtiennes une réponse pour la bonne raison que le groupe multiplicatif des élements inversibles de Z/nZ n'est pas toujours cyclique!
Prend par exemple Z/15Z, Il y a bien phi(15)=8 éléments inversibles: (1,2,4,7,8,11,13,14) mais pas de cycle: outre 1, deux éléments 4 et 14 sont leurs propres inverses, ce qui est impossible dans un groupe cyclique!

Je me suis justement reconnecté pour dire que je n'etais meme pas sur en fait que (Z/nZ)* soit toujours cyclique.

Par ailleurs, j'avoue donc le caractere peremptoire de ma proposition. Je paraissais juste un peu sur de ca! Une apparence de verité quoi! J'ai commis la une entorse aux methodes mathematiques qui veut que l'on prouve d'abord avant de declarer!

Mais aussi, je ferai juste remarquer un petit probleme, celui qui advient quand on pense reussir une preuve qu'on s'est faite soi meme sur papier ou avec l'aide d'un autre camarade... et qui est en faite fausse. On devient alors certain de son resultat et on le propose aux autres, jusqu'a ce que quelqu'un y trouve un os. Cela a ete le cas mon affirmation concernant (Z/nZ)*.

Merci.

"Max de respects à tout le monde."

par **Alpha** » 19 Aoû 2005, 22:34

Salut, RadarX!

Ne t'en fais pas, il n'y a aucun problème :happy3:.

N'aie aucune crainte! Tu es un membre tout à fait respectable.

Et c'est un modérateur qui te le dit.

Cependant, la prochaine fois, évite de créer un nouveau poste pour reposer une même question : si tu veux relancer la discussion, poste un message à la suite de la discussion d'origine.

Cordialement :happy3:

par **RadarX** » 19 Aoû 2005, 22:41

Non bleme Alpha! Ca fait plaisir :we:

RadarX!

par **Alpha** » 19 Aoû 2005, 22:43

Salut, RadarX, j'ai supprimé la nouvelle discussion que tu avais postée et à la place j'ai changé le nom de cette discussion-là.

Si tu veux modifier le nom d'une discussion que tu as postée, il te suffit de modifier ton message.

Merci de ta compréhension. :happy3:

par **RadarX** » 20 Aoû 2005, 10:55

palmade a écrit:Malgré le ton péremptoire de la demande,

(EDIT Alpha (modérateur) : le titre original de la discussion n'était pas le titre actuel)

il serait étonnant que tu obtiennes une réponse pour la bonne raison que le groupe multiplicatif des élements inversibles de Z/nZ n'est pas toujours cyclique!
Prend par exemple Z/15Z, Il y a bien phi(15)=8 éléments inversibles: (1,2,4,7,8,11,13,14) mais pas de cycle: outre 1, deux éléments 4 et 14 sont leurs propres inverses, ce qui est impossible dans un groupe cyclique!

Je me suis expliqué sur le titre (c'est vrai un peu trop) categorique. Je disais qu'il n'y avait rien de pretentieux venant de ma part; c'etait juste pour relancer ma question et non pour insister sur le fait que (Z/nZ)* etait cyclique. C'est Alpha qui a lu mon explication et a changé le titre pour remettre de l'ordre.

Par ailleurs as-tu une preuve du fait que dans un groupe cyclique, un element different du neutre ne peut pas etre son propre symetrique?

RadarX.

par **Anonyme** » 20 Aoû 2005, 12:14

@Dans Z/4Z, qui est cyclique, 2 est son propre symétrique.

@@Ce que tu croyais vrai dans tout Z/nZ est quand même vrai quand n est premier : (Z/pZ)* est le groupe cyclique d'ordre p-1

par **Alpha** » 20 Aoû 2005, 12:37

Salut, sept-épées,

Je ne comprends pas ton @@ :

On ne dit pas d'un groupe qu'il a un certain ordre, on dit qu'un élément d'un groupe a un certain ordre.

:happy3:

par **Alpha** » 20 Aoû 2005, 12:43

Pour RadarX,

ce qu'il faut comprendre dans ce qu'a dit palmade, ce n'est pas que si (Z/nZ)* est cyclique, un élément de (Z/nZ)* ne peut pas être son propre symétrique, mais que si (Z/nZ)* est cyclique, on ne peut pas trouver 2 éléments distincts de (Z/nZ)* qui soient chacun leur propre inverse.

:happy3:

par **RadarX** » 20 Aoû 2005, 13:18

Alpha a écrit:Pour RadarX,

ce qu'il faut comprendre dans ce qu'a dit palmade, ce n'est pas que si (Z/nZ)* est cyclique, un élément de (Z/nZ)* ne peut pas être son propre symétrique, mais que si (Z/nZ)* est cyclique, on ne peut pas trouver 2 éléments distincts de (Z/nZ)* qui soient chacun leur propre inverse.

:happy3:

Le contre exemple de 7-epees, tient bien la route avec Z/4Z.
Mais c'est vrai que son @@ est un peu ambigue: alors si tu peux nous eclaircir un peu.
Par ailleurs une autre interpretation de l'affirmation de Palmade s'impose alors.
Pour Alpha, je ne vois la meme chose que toi dans ce qu'il dit; il a bien dit "outre 1 (donc l'element neutre de (Z/nZ)*), 4 et 14 sont ..."
Alors est ce que c'est qu'on ne puisse pas avoir 2 elements qui soient leurs propres inverses (comme le pense Alpha) ou bien c'est qu'on ne peut avoir 2 autres elements differents du neutre (donc 3 elements) qui soient leurs propres inverses.

Dans tous les cas une petite preuve leverait tout equivoque

par **palmade** » 20 Aoû 2005, 14:01

Dans un groupe cyclique de générateur g d'ordre pair 2p, g^(2p)=e (neutre); h=g^p est tel que h^2=e (auto-inverse) et quel que soit 0On ne peut donc avoir qu'un seul élément auto-inverse en plus du neutre.
Si l'ordre est impair, il n'y a que le neutre...

par **Alpha** » 20 Aoû 2005, 17:48

Dans ma réponse, il était sous-entendu "éléments différents de l'élément neutre". Ca allait tellement de soi que je n'ai pas pensé à le préciser.

par **Alpha** » 20 Aoû 2005, 17:50

Je confirme par ailleurs la réponse de palmade. Ce qu'il a dit est l'évidence même! Mais ce qui va sans dire va parfois mieux en le disant...

par **Zeitblom** » 20 Aoû 2005, 21:29

Pour les gens que ça intéresse, http://www.les-mathematiques.net/b/a/d/node19.php3 prouve que (Z/pZ)* est cyclique pour p premier (c'est pas vraiment trivial), et indique sur une autre page que le problème d'en trouver un générateur pour p quelconque n'est pas résolu.

par **RadarX** » 20 Aoû 2005, 22:37

:mur: Dire que je me suis cassé la tete pour essayer de le prouver!!!
En tout cas je suis maintenant bien edifié! Sympa les gars.
Merci aussi a Zeitblom pour le site sur (Z/nZ)*.

RadarX.

par **Anonyme** » 21 Aoû 2005, 17:39

salut alpha,

on appelle "ordre" d'un groupe fini son cardinal.

par **Alpha** » 21 Aoû 2005, 18:31

Faux, sept epees! :marteau:

A moins que nous n'ayons pas la même définition de l'ordre, ou que ce mot corresponde à deux notions très différentes, ce qui est rare en mathématiques, je ne suis pas d'accord avec toi.

L'ordre d'un élément g d'un groupe G est le plus petit entier n strictement positif tel que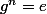

.

S'il se trouve que le groupe est fni et monogène (c'est à dire cyclique), il se trouve alors que le cardinal de ce groupe, qui est alors le groupe engendré par un élément, le générateur g, est aussi l'ordre de cet élément g, mais seulement dans ce cas.

Donc un groupe fini a un cardinal égal à l'ordre d'un de ses éléments si et seulement si ce groupe est le groupe engendré par cet élément.

Cordialement

par **Zeitblom** » 21 Aoû 2005, 20:07

Fais une recherche avec "ordre d'un groupe" sur Google, tu verras que ca existe bien, et que c'est très usuel :)

Petit rappel terminologique :
-On appelle ordre d'un élément dans un groupe (disons fini) le cardinal du sous groupe engendré par ledit élément, ce qui correspond à ta définition.
-On appelle ordre d'un groupe fini le cardinal de ce groupe.

C'est donc deux notions différentes, qu'on peut relier par le résultat suivant : dans un groupe fini, l'ordre de tout élément divise l'ordre du groupe. On sait même que si p est un diviseur premier de l'ordre du groupe, il existe un élément d'ordre p dans le groupe.

par **Alpha** » 21 Aoû 2005, 21:17

Personnellement, dès que deux choses sont nettement différentes, je préfère employer deux termes différents pour les désigner. Et si les choses sont nettement différentes, mais qu'en plus elles s'emploient dans un même contexte, je trouve que c'est assez grave, car cela porte naturellement à confusion.

Mais, malheureusement, les mathématiques ont encore, à ce que je vois, quelques imperfections à ce niveau là.

Pour que les choses soient les plus claires possibles, il est évident qu'il faut qu'il existe une bijection entre l'ensemble des termes et l'ensemble des notions mathématiques!

Une question sur (Z/nZ)* please

Une question sur (Z/nZ)* please

remarques

ordre d'un groupe

Qui est en ligne