Une question sur les tests
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Dante0
- Membre Irrationnel
- Messages: 1243
- Enregistré le: 15 Nov 2010, 21:20
-
 par Dante0 » 02 Jan 2014, 00:58
par Dante0 » 02 Jan 2014, 00:58
Bonsoir,
J'ai une petite question concernant les tests qui a son importance.
On se propose de construire un test UPP de

contre

avec

sur un echantillon iid de taille n issu d'une loi normale
On utilise le lemme de neyman pearson et on trouve finalement que notre zone de rejet est de la forme :

On fait notre petite cuisine et on arrive à :
 = \alpha)
La zone de rejet est donc
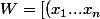\in R^n : \frac{\bar{X_n}-\mu_0}{\frac{\sigma}{\sqrt{n}}} \geq z_{1-\alpha}])
Maintenant on suppose qu'on a une hypothèse alternative

tel que

On aurait obtenu la région de rejet suivante :
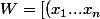\in R^n : \frac{\bar{X_n}-\mu_0}{\frac{\sigma}{\sqrt{n}}} \leq z_{\alpha}])
Je ne comprends pas comment on l'obtient et pourquoi on a

cette fois ci ?
D'ailleurs pour moi c'est équivalent puisque

non ?
Merci !
-
Sylviel
- Membre Transcendant
- Messages: 6466
- Enregistré le: 20 Jan 2010, 12:00
-
 par Sylviel » 02 Jan 2014, 10:24
par Sylviel » 02 Jan 2014, 10:24
C'est toujours pareil : tu choisis ta zone de rejet de manière à minimiser l'erreur de seconde espèce. Intuitivement tu prends la zone qui a le plus de chance de se réaliser sous l'hypothèse alternative.
Si mu1 est plus grand que mu0 ta moyenne empirique (sous l'hypothèse alternative) devrait être plus grande aussi, tu choisis donc la zone des "grandes moyenne empirique" comme zone de rejet. Si mu1 est plus petit que mu0, la moyenne empiirique sous l'hyp alternative serait logiquement plus petite, tu choisit donc comme zone de rejet la zone des petits résultats.
Le lien entre -z_a et z_(1-a) n'existe qu'à cause de la symétrie de la distribution gaussienne. Mais cela ne donne pas le même résultat : le signe est inversé...
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
-
Dante0
- Membre Irrationnel
- Messages: 1243
- Enregistré le: 15 Nov 2010, 21:20
-
 par Dante0 » 02 Jan 2014, 16:12
par Dante0 » 02 Jan 2014, 16:12
Sylviel a écrit:C'est toujours pareil : tu choisis ta zone de rejet de manière à minimiser l'erreur de seconde espèce. Intuitivement tu prends la zone qui a le plus de chance de se réaliser sous l'hypothèse alternative.
Si mu1 est plus grand que mu0 ta moyenne empirique (sous l'hypothèse alternative) devrait être plus grande aussi, tu choisis donc la zone des "grandes moyenne empirique" comme zone de rejet. Si mu1 est plus petit que mu0, la moyenne empiirique sous l'hyp alternative serait logiquement plus petite, tu choisit donc comme zone de rejet la zone des petits résultats.
Le lien entre -z_a et z_(1-a) n'existe qu'à cause de la symétrie de la distribution gaussienne. Mais cela ne donne pas le même résultat : le signe est inversé...
La moyenne empirique c'est bien X_n ?
Si mu1 > mu0 elle devrait être plus petite alors sous l'hypothèse alternative non ?

donc ca revient au même non ?
-
Sylviel
- Membre Transcendant
- Messages: 6466
- Enregistré le: 20 Jan 2010, 12:00
-
 par Sylviel » 02 Jan 2014, 16:21
par Sylviel » 02 Jan 2014, 16:21
La moyenne empirique c'est bien \bar X_n, elle est "proche" de l'espérance.
Sous l'hypothèse alternative elle est "proche" de mu1...
Dans ta suite d'équivalence tu as changé un signe de l'inégalité et pas l'autre !
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
-
Dante0
- Membre Irrationnel
- Messages: 1243
- Enregistré le: 15 Nov 2010, 21:20
-
 par Dante0 » 02 Jan 2014, 18:02
par Dante0 » 02 Jan 2014, 18:02
Sylviel a écrit:La moyenne empirique c'est bien \bar X_n, elle est "proche" de l'espérance.
Sous l'hypothèse alternative elle est "proche" de mu1...
Dans ta suite d'équivalence tu as changé un signe de l'inégalité et pas l'autre !
POurquoi est-ce qu'on aurait tout simplement pas obtenu
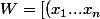\in R^n : \frac{\bar{X_n}-\mu_0}{\frac{\sigma}{\sqrt{n}}} \leq z_{1-\alpha}])
dans le cas ou :

? C'est qu'une inégalité qui change de sens, je comprends pas pourquoi on s'intéresse à un autre quartile..
Elle est ou mon erreur, je n'en vois pas ?
-
Sylviel
- Membre Transcendant
- Messages: 6466
- Enregistré le: 20 Jan 2010, 12:00
-
 par Sylviel » 02 Jan 2014, 18:08
par Sylviel » 02 Jan 2014, 18:08
Parce que ce W là pèse pour 1-alpha, donc tu as une zone de rejet de 95% au lieu d'une zone de rejet de 5%, donc ton erreur de première espèce est de 95%...
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
-
Dante0
- Membre Irrationnel
- Messages: 1243
- Enregistré le: 15 Nov 2010, 21:20
-
 par Dante0 » 02 Jan 2014, 19:31
par Dante0 » 02 Jan 2014, 19:31
Sylviel a écrit:Parce que ce W là pèse pour 1-alpha, donc tu as une zone de rejet de 95% au lieu d'une zone de rejet de 5%, donc ton erreur de première espèce est de 95%...
Je ne comprends pas "W pèse pour 1-alpha" ? :doh:
Oui alpha = 0,05 donc ca correspond bien à un risque de 5%
Mais la je suis complètement perdu, je vois pas du tout le lien, j'aurais été en DS j'aurais écrit :
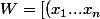\in R^n : \frac{\bar{X_n}-\mu_0}{\frac{\sigma}{\sqrt{n}}} \leq z_{1-\alpha}])
Au lieu de
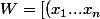\in R^n : \frac{\bar{X_n}-\mu_0}{\frac{\sigma}{\sqrt{n}}} \leq z_{\alpha}])
Sinon qu'est-ce qui est faux dans mon raisonnement du dessus ? :hein:
Je suis lent à la détente mais je finirais bien par comprendre...
-
Sylviel
- Membre Transcendant
- Messages: 6466
- Enregistré le: 20 Jan 2010, 12:00
-
 par Sylviel » 02 Jan 2014, 19:34
par Sylviel » 02 Jan 2014, 19:34
Et bien le W que tu as écrit est tel que P(W) = 0.95. Donc même si ton hypothèse est bonne ton test la refuseras 95% du ton (et non 5% du temps), ce qui veux dire que ton risque de première espèce est de 95% et non de 5%.
Tu peux le voir ainsi, sous l'hypothèse H0 ton test est pratiquement une Gaussienne. Et là ta zone de rejet au lieu d'être un bout de la gaussienne c'est l'ensemble sauf l'extrêmité de droite.
Alors qu'en vrai tu veux que la zone de rejet soit le petit bout à gauche...
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
-
Dante0
- Membre Irrationnel
- Messages: 1243
- Enregistré le: 15 Nov 2010, 21:20
-
 par Dante0 » 03 Jan 2014, 01:47
par Dante0 » 03 Jan 2014, 01:47
J'ai pas compris tes explications, surement du au fait que je n'ai pas compris les concepts inhérents, mais peu importe, je viens de me rendre compte de ma sottise, j'avais déja compris ce problème la en fait.
Merci pour l'intervention en tout cas ! :we:
-
Sylviel
- Membre Transcendant
- Messages: 6466
- Enregistré le: 20 Jan 2010, 12:00
-
 par Sylviel » 03 Jan 2014, 08:51
par Sylviel » 03 Jan 2014, 08:51
Je réessaie une explication que je t'ai déjà donnée (mais à mon avis tu as pas mal de lacune sur les probas (quand je vois l'autre fil) ce qui rends la compréhension des tests plus ardue...).
Lorsque tu construit un test tu choisis 2 Hypothèse : H0 et H1.
Un test à 5% consiste à construire un ensemble d'évènement élémentaires W, appelé zone de rejet, tel que la probabilité de cet ensemble, sous l'hypothèse H0, soit de 5%. Si un évènement de W se réalise ton test t'indiqueras que "H0 n'est pas vraie". Tu as donc 5% de chance de déclarer H0 fausse alors qu'elle est vraie, c'est ce qu'on appelle le risque de première espèce.
L'idée pour choisir cette zone qui "pèse" 5%, donc tel que P(W)=5%, c'est de prendre celle qui a le plus de chance de se réaliser sous H1.
Dans ton exemple le W que tu proposais pesait 95% et non 5%. Donc même si H0 était vraie ton test la déclarerait fausse 95% du temps...
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 47 invités
