Une intégrale assez coriace
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
zwijndrecht
- Membre Naturel
- Messages: 83
- Enregistré le: 29 Oct 2020, 12:13
-
par zwijndrecht » 04 Nov 2024, 17:26
Bonjour,
Je cherche à calculer l'intégrale suivante :
\sin(x) + 8 \cos^3(x)\sin^2(x)+2 \cos(x)\sin^2(x) + 8 \cos^2(x)\sin^3(x) \right]\sqrt{2 \cos(x)\sin(x)}\mathrm{d}x)
J'ai tenté d'utiliser les formules d'arc-moitié (en général, ça fonctionne pour les intégrales trigonométriques récalcitrantes), mais la racine carrée continue de poser problème...
Voyez-vous comment faire ?
Merci d'avance.
vam edit > j'ai enlevé les balises latex pour qu'on puisse lire2e edit > Latex étant reparti 
je remets les balises
-
Pisigma
- Habitué(e)
- Messages: 3108
- Enregistré le: 21 Déc 2014, 23:38
-
par Pisigma » 04 Nov 2024, 17:36
Bonjour,
on a pas l'énoncé!
-
Pisigma
- Habitué(e)
- Messages: 3108
- Enregistré le: 21 Déc 2014, 23:38
-
par Pisigma » 04 Nov 2024, 17:48
je viens de me rendre compte qu'il y a un problème avec le Latex; je t'invite à joindre ton énoncé en passant par un hébergeur d'images
-
vam
- Admin
- Messages: 636
- Enregistré le: 09 Aoû 2019, 09:50
-
par vam » 04 Nov 2024, 20:34
Bonsoir
en attendant que le Ltx refonctionne, j'ai enlevé les balises pour que ce soit lisible
les informaticiens travaillent dessus, mais la panne est un peu musclée cette fois, ce n'est pas un simple serveur à faire redémarrer comme les autres fois.
Pour mettre une image, vous pouvez aller sur
https://postimages.org/fr/Vous choisirez ce qu'ils appellent le lien direct (lien de la seconde ligne), que vous placerez entre les balises Img.
-
catamat
- Habitué(e)
- Messages: 1283
- Enregistré le: 07 Mar 2021, 10:40
-
par catamat » 04 Nov 2024, 22:24
Bonjour
Avec un editeur latex j'obtiens ça :
-
Pisigma
- Habitué(e)
- Messages: 3108
- Enregistré le: 21 Déc 2014, 23:38
-
par Pisigma » 05 Nov 2024, 15:05
merci catamat !
une piste: en transformant un peu l'expression entre crochets, et sauf erreur de ma part, il vient [sin(2x)(cos(x)+sin(x))+sin^2(2x)(sin(x)+cos(x))]racine(sin(2x))
multiplier l'expression entre crochets par la racine, ensuite scinder l'expression en 2 et poser sin(x)-cos(x)=u
-
catamat
- Habitué(e)
- Messages: 1283
- Enregistré le: 07 Mar 2021, 10:40
-
par catamat » 05 Nov 2024, 16:06
De rien
PisigmaJ'avais fait grosso modo la même chose, mais j'ai un facteur 2 en plus (sauf erreur bien sûr)
Soit C le crochet
C=2sin x cos x(cos x + 4 cos²x sin x +sin x +4 cos x sin²x)
=2sin x cos x(cos x +sin x)(1 +4 cos x sinx)
=sin(2x)(cos x +sin x)(1 +2sin(2x))
=sin(2x)(cos x +sin x) + 2sin²(2x) (cos x +sin x)
Ensuite j'avais pensé à faire passer la racine au dénominateur car elle s'écrit
ce qui est sympa pour intégrer... mais je n'ai pas poussé jusqu'au bout.
-
Pisigma
- Habitué(e)
- Messages: 3108
- Enregistré le: 21 Déc 2014, 23:38
-
par Pisigma » 05 Nov 2024, 18:20
effectivement, j'ai oublié de recopier un 2; finalement j'ai
(cos(x)+sin(x))+\textcolor{\red}{2}sin^2(2x)(sin(x)+cos(x))]racine(sin(2x)))
avant d'en montrer un peu plus, attendons le retour du posteur!
-
Pisigma
- Habitué(e)
- Messages: 3108
- Enregistré le: 21 Déc 2014, 23:38
-
par Pisigma » 05 Nov 2024, 21:20
en posant
-cos(x)=u)
on trouve
-
zwijndrecht
- Membre Naturel
- Messages: 83
- Enregistré le: 29 Oct 2020, 12:13
-
par zwijndrecht » 06 Nov 2024, 22:46
Merci pour vos réponses.
Je suis d'accord sur le fait que le crochet fait bien
(\cos x +\sin x) + 2 \sin^2(2x) (\cos x +\sin x))
Ensuite, si je pose
)
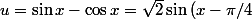, j'obtiens
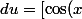 + \sin(x) \right] dx)
et
=\cos\left(\pi/2 - 2x) = \cos\left[2 \left(\pi/4 - x\right)\right]=1- 2 \sin^2 \left(x - \pi/4) = 1-2 \left(u/\sqrt{2}\right)^2 = 1-u^2)
In fine, on a donc (sauf erreur de ma part)
 \left[ \cos(x)+\sin(x)\right] \sqrt{\sin(2x)} dx = \int_{-1}^{1} (1-u^2) \sqrt{1-u^2} du)
.
Et je ne vois pas trop comment intégrer ça... sauf à poser
)
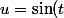, mais on tourne en rond du coup, non ?
-
zwijndrecht
- Membre Naturel
- Messages: 83
- Enregistré le: 29 Oct 2020, 12:13
-
par zwijndrecht » 06 Nov 2024, 23:14
En posant
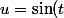, je me retrouve en fait à intégrer
)
(et ça, je sais faire en faisant une IPP). Mais est-ce que je ne suis pas compliqué la vie en faisant tout ça ? (le coup de faire disparaître les fonctions trigo pour les faire réapparaître aussi sec me laisse un peu perplexe...)
-
Pisigma
- Habitué(e)
- Messages: 3108
- Enregistré le: 21 Déc 2014, 23:38
-
par Pisigma » 07 Nov 2024, 08:14
je réponds à la question sur
)
il suffit de linéariser
. Tu peux passer par
=\left(\dfrac{e^{i t}+e^{-it}}{2}\right)^4)
avec un exposant
c'est la méthode généralement employée
-
Pisigma
- Habitué(e)
- Messages: 3108
- Enregistré le: 21 Déc 2014, 23:38
-
par Pisigma » 07 Nov 2024, 13:19
sorry! je voulais écrire avec un exposant
-
catamat
- Habitué(e)
- Messages: 1283
- Enregistré le: 07 Mar 2021, 10:40
-
par catamat » 09 Nov 2024, 11:06
Ok pour revenir à la trigo mais il y a un truc que je ne comprends pas.
En fait, si on demande une primitive de f telle que
=(1-u^2) \sqrt{1-u^2})
a un logiciel de calcul formel il sort ceci
=\dfrac{1}{8}[\sqrt{1-u^2}(5u-2u^3)+3 sin^{-1}(u)])
Effectivement si on dérive on retrouve f, mais je ne vois pas la méthode utilisée... si quelqu'un connait.
-
Pisigma
- Habitué(e)
- Messages: 3108
- Enregistré le: 21 Déc 2014, 23:38
-
par Pisigma » 09 Nov 2024, 20:00
@catamat: peut-être en procédant comme suit , mais ça me paraît un peu tordu!
en scindant l'intégrale:
posons
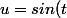 \,[t=arcsin(u)])
en développant, il vient
}{2}dt=\dfrac{t}{2}+\dfrac{sin(2t)}{4}=\dfrac{1}{2}\left[arcsin(u)+\dfrac{1}{2}sin(2\,arcsin(u))\right])
Il reste à calculer
-
catamat
- Habitué(e)
- Messages: 1283
- Enregistré le: 07 Mar 2021, 10:40
-
par catamat » 10 Nov 2024, 19:14
Bon je ne sais pas si la méthode employée par les logiciels (c'est assez galère...) mais en fait f(u) peut s'écrire ainsi :
=\dfrac{(1-u^2)^2}{\sqrt{1-u^2}}=\dfrac{u^4-2u^2+1}{\sqrt{1-u^2}})
La partie
est la dérivée de arcsin(u)
et la partie
=\dfrac{u^4-2u^2}{\sqrt{1-u^2}})
est la dérivée d'une fonction G produit d'un polynôme par
Reste à trouver le polynôme, comme le polynôme de sa dérivée est pair et degré 4, le polynôme de la primitive sera impair (on verra que le degré 3 est suffisant)
La primitive cherchée est donc de la forme
=(au^3+bu) \sqrt{1-u^2})
On a
=(au^3+bu) \dfrac{-u}{\sqrt{1-u^2}}+(3au^2+b)\sqrt{1-u^2})
ou encore
=\dfrac{-au^4-bu^2}{\sqrt{1-u^2}}+\dfrac{(3au^2+b)(1-u^2)}{\sqrt{1-u^2}})
=\dfrac{-4au^4+(3a-2b)u^2+b}{\sqrt{1-u^2}})
Si on identifie les termes de degré 4 et 2 des numérateurs de G'(u) et f(u) il vient
-4a=1 et 3a-2b=-2
d'où a=-1/4 et b =5/8
Donc si
=(\frac{-1}{4}u^3+\frac{5}{8}u) \sqrt{1-u^2})
on a
=\dfrac{u^4-2u^2+\frac{5}{8}}{\sqrt{1-u^2}}=f(u)-\dfrac{\frac{3}{8}}{\sqrt{1-u^2}})
Finalement
F(u)=G(u)+(3/8)arcsin(u) soit le résultat donné par le logiciel...
-
catamat
- Habitué(e)
- Messages: 1283
- Enregistré le: 07 Mar 2021, 10:40
-
par catamat » 11 Nov 2024, 11:20
Cela marche aussi pour la première partie de l'intégrale de départ soit pour
=2(1-u^2)^2\sqrt{1-u^2})
qui peut s'écrire
=\dfrac{2(1-u^2)^3}{\sqrt{1-u^2}}=\dfrac{-2u^6+6u^4-6u^2+2}{\sqrt{1-u^2}})
Dans ce cas
=(au^5+bu^3+cu)\sqrt{1-u^2})
et
=\dfrac{-6ax^6+(5a-4b)x^4+(3b-2c)x^2+c}{\sqrt{1-u^2}})
L'identification donne -6a=-2, 5a-4b=6 et 3b-2c=-6
d'où a=1/3, b=-13/12 et c= 11/8
Donc
=(\frac{1}{3}u^5-\frac{13}{12}u^3+\frac{11}{8}u)\sqrt{1-u^2})
et
=G'(u)+\dfrac{\frac{5}{8}}{\sqrt{1-u^2}})
donc F(u)=G(u)+5/8 arcsin(u)
-
Pisigma
- Habitué(e)
- Messages: 3108
- Enregistré le: 21 Déc 2014, 23:38
-
par Pisigma » 12 Nov 2024, 10:56
-
catamat
- Habitué(e)
- Messages: 1283
- Enregistré le: 07 Mar 2021, 10:40
-
par catamat » 12 Nov 2024, 15:55
Merci beaucoup Pisigma pour ce nécessaire (du moins pour moi) rappel des fondamentaux.
On trouve en effet la même chose, en utilisant les formules classiques de trigo.
-
Pisigma
- Habitué(e)
- Messages: 3108
- Enregistré le: 21 Déc 2014, 23:38
-
par Pisigma » 13 Nov 2024, 11:00
catamat : ta méthode était plus recherchée ; j'ai appris quelque chose; dans mes souvenirs, je crois que je n'étais jamais passé par le calcul d'une dérivée, merci!
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 43 invités
