Exercice coriace d'algebre

par **lomdefer** » 14 Oct 2006, 19:49

Soit

un ensemble quelconque. On note

l'ensemble des parties de

. Soit

une application de

dans

.
On pose :

a)
Montrer que

Je sais que

est la reciproque de

mais je ne sais vraiment pas par ou commencer...

par **tize** » 14 Oct 2006, 19:58

lomdefer a écrit:Soit un ensemble quelconque. On note l'ensemble des parties de . Soit une application de dans .
On pose :

a)
Montrer que
Je sais que est la reciproque de mais je ne sais vraiment pas par ou commencer...

C'est un classique pour montrer Cantor-Bernstein : il n'y a pas de bijection de X dans P(x)...

Suppose le contraire :

, il existe alors

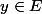
tq

et poses toi la question suivante : est ce que

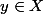
? Tu vas tomber sur un absurdité

par **Yipee** » 14 Oct 2006, 20:15

Euh... Ce n'est pas du tout le théorème de Cantor-Bernstein. Ce dernier dit que s'il y a une injection de X dans Y et une injection de Y dans X alors X et Y sont équipotent. C'est bien plus difficile à démontrer...

par **BiZi** » 14 Oct 2006, 20:20

Ca s'appelle le théorème de Cantor le résultat de cet exo, mais la confusion est pardonnable :lol4:

par **lomdefer** » 14 Oct 2006, 20:22

Déja je n'arrive pas trop a comprendre ce que veux dire :

est-ce que

est un ensemble ?
dans ce cas la :

par **BiZi** » 14 Oct 2006, 20:25

En fait c'est la chose la plus difficile à comprendre dans cette exo. Ca peut paraître étrange, mais c'est simplement que x est un élément de E, et f(x) est une partie de E; il est donc tout-à-fait possible que f(x) contienne x.

par **lomdefer** » 14 Oct 2006, 20:27

dsl je doit partir merci pour votre aide je revien demain pour plus de precision.
Merci

par **tize** » 14 Oct 2006, 20:40

BiZi a écrit:Ca s'appelle le théorème de Cantor le résultat de cet exo, mais la confusion est pardonnable :lol4:

Oui merci...c'est vieux pour moi tout ça. Merci de m'avoir corrigé une fois de plus Yipee et Bizi

par **mejdane** » 14 Oct 2006, 22:53

par définition on a si f est une application de E ds F alors il existe un et un seul y appartenant à F tel que f(x)=y.
Est ce que ça ne s'oppose pas à dire supposer que f(x) est une partie de l'ensemble P(E)?

par **mejdane** » 14 Oct 2006, 22:57

mejdane a écrit:par définition on a si f est une application de E ds F alors il existe un et un seul y appartenant à F tel que f(x)=y.
Est ce que ça ne s'oppose pas à dire supposer que f(x) est une partie de l'ensemble P(E)?

je retiend ma remarque :
f(x) est une partie de E pas de P(E)!

par **MooMooBloo** » 15 Oct 2006, 09:15

n'est PAS la réciproque de

! F n'a aucune raison d'etre bijective...

par **lomdefer** » 15 Oct 2006, 16:24

tout sa ne me dit pas comment montrer que

.
Je comprend rien a ce que vous dite...dsl

par **abcd22** » 15 Oct 2006, 16:42

Bonjour,
Tize a dit comment montrer

dans la première réponse.
f est une application de E dans P(E), par exemple avec E = {0,1} on pourrait avoir f(0) = {1} et f(1) = {0,1} = E, on a donc

et

.
X est une partie de E, et on se demande si elle est dans l'image de f.

Exercice coriace d'algebre

exercice coriace d'algebre

Qui est en ligne