x ^2- 2 y^2 + xy + 2 = 0
resoudre l equation
J ai essayé de factoriser mais j arrive pas a effectuer la factorisation nécessaire et la je doute Qu il s agit d une factorisation , y a-t-il une facons rapide pour l a resoudre ?!
Une equation VS deux inconnu...
11 messages
- Page 1 sur 1
Re: Une equation VS deux inconnu...
salut
l'énoncé est très imprécis ...
résoudre ... où ? dans R ...
tu peux considérer que tu as un trinome du second degré en x ... ou en y ...
ainsi par exmple ...
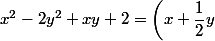^2 - \left( \dfrac 9 4 y^2 - 2 \right) = 0)
pour exprimer x en fonction de y il suffit que le second terme soit positif ...(donc te donne un ensemble de valeur pour y) ...
ensuite on peut faire la même chose en permutant x et y ...
l'énoncé est très imprécis ...
résoudre ... où ? dans R ...
tu peux considérer que tu as un trinome du second degré en x ... ou en y ...
ainsi par exmple ...
pour exprimer x en fonction de y il suffit que le second terme soit positif ...(donc te donne un ensemble de valeur pour y) ...
ensuite on peut faire la même chose en permutant x et y ...
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Re: Une equation VS deux inconnu...
A oui en se que concerne la solution c est dans z ^2 , donc je les solution doive appartenir a z...
Re: Une equation VS deux inconnu...
s'il existe des entiers a, b et c tels que 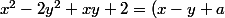(x + 2y + b) + c) alors c'est fini ...
alors c'est fini ...
à toi de développer et d'identifier ...
à toi de développer et d'identifier ...
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Re: Une equation VS deux inconnu...
... ce qui nous avance beaucoup pour trouver les solutions entières. 

Re: Une equation VS deux inconnu...
Bonjour;
Comme on a : = 0) une équation de second degré en x, dont
une équation de second degré en x, dont 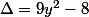 .
.
Pour que cette équation ait des solutions dans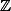 , il faut que
, il faut que  soit un carré parfait .
soit un carré parfait .
Soit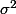 ce carré parfait , donc on a : 9
ce carré parfait , donc on a : 9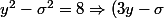(3y+\sigma)=8) .
.
En traitant les huit cas possibles on trouve que l'ensemble des solutions est :;(-1,1);(0,-1);(1,-1)\}) .
.
J'espère que je ne dis pas des bêtises.
Comme on a :
Pour que cette équation ait des solutions dans
Soit
En traitant les huit cas possibles on trouve que l'ensemble des solutions est :
J'espère que je ne dis pas des bêtises.
Re: Une equation VS deux inconnu...
Aymane, tu ne peux vraiment pas t'empêcher de traiter les exercices à la place des questionneurs ? (Et avec une méthode qui est loin d'être optimale).
Re: Une equation VS deux inconnu...
Merci énormément.. J ai trouvé les meme 4 solutions merci.. (en utilisant la factorisation)
11 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 24 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
