TVI
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)

-
chombier
- Membre Irrationnel
- Messages: 1324
- Enregistré le: 19 Juil 2012, 18:35
-
 par chombier » 21 Sep 2024, 11:04
par chombier » 21 Sep 2024, 11:04
Bonjour
J'ai une petite question à propos du TVI.
Soit

une fonction continue vérifiant
=0)
et
=3)
J'affirme que pour tout

, l'équation
=y)
admet au moins une solution.
Le TVI ne s'applique pas car

n'est pas un segment.
Comment prouver mon affirmation ? J'ai bien quelques pistes mais je les trouve bien compliquées.
Vos idées m'intéressent beaucoup, merci d'avance !!
En terminale, les profs n'ont pas d'états d'âme


Source : un corrigé de l'apmep
https://www.apmep.fr/IMG/pdf/Corrige_sp ... 024_BS.pdf

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 21 Sep 2024, 11:16
par Ben314 » 21 Sep 2024, 11:16
Salut,
Si

alors, par définition de ce que signifie
\!=\!3)
, il existe un réel

tel que, pour tout

, on ait
\!\geqslant\!y)
. Il suffit ensuite d'appliquer le T.A.F. au segment
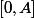
.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius

-
chombier
- Membre Irrationnel
- Messages: 1324
- Enregistré le: 19 Juil 2012, 18:35
-
 par chombier » 21 Sep 2024, 11:30
par chombier » 21 Sep 2024, 11:30
Merci Ben, c'est ce que j'avais à peu près en tête sauf que j'avais ajouté un

et j'avais appliqué la définition formelle de la limite en

.
Que penses-tu du corrigé ?
J'enseigne en terminale et je suis toujours mal à l'aise avec ça (j'applique la méthode du corrigé que je considère tout simplement comme fausse

).

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 21 Sep 2024, 11:36
par Ben314 » 21 Sep 2024, 11:36
Je connais pas trop les programmes, ni le niveau actuel au Lycée, donc j'en pense pas grand chose . . .
Pour quelqu'un qui aurais compris la définition d'une limite, ce type de rédaction ne pose pas de problème, mais vu que je suppose que ce n'est pas trop le cas du terminale de base . . .
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius

-
vam
- Admin
- Messages: 681
- Enregistré le: 09 Aoû 2019, 09:50
-
 par vam » 21 Sep 2024, 12:32
par vam » 21 Sep 2024, 12:32
Bonjour
Bon, un élève qui rédigera ça comme ça, aura ses points, OK
Mais je pense, une fois qu'on a vu dans quel secteur cela était possible, il n'est pas interdit de prendre de prendre deux valeurs du genre 0 et 2, de dire avant 0 rien, après 2 rien non plus, et de mettre en valeur f(0) et f(2). Et là on peut appliquer plus proprement. Non ?
Pour mettre une image, vous pouvez aller sur
https://postimages.org/fr/Vous choisirez ce qu'ils appellent le lien direct (lien de la seconde ligne), que vous placerez entre les balises Img.


-
chombier
- Membre Irrationnel
- Messages: 1324
- Enregistré le: 19 Juil 2012, 18:35
-
 par chombier » 21 Sep 2024, 13:00
par chombier » 21 Sep 2024, 13:00
Voila comment je rédigerais si je voulais détailler toutes les étapes :
Soit

.
Par définition de la limite,
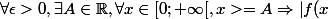-3 \right| < \epsilon)

donc il existe un réel A tel que
-3 \right| < 3-y)
En particulier, avec
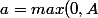)
,
-3 \right|>3-y)
donc
-3 > y-3)
donc
>y)
.
<=y)
et
>=y)
donc on peut appliquer le TVIà l'intervalle [0;a]
C'est la preuve de Ben314 avec plus de détails sur l'existence du "A"

-
vam
- Admin
- Messages: 681
- Enregistré le: 09 Aoû 2019, 09:50
-
 par vam » 21 Sep 2024, 13:54
par vam » 21 Sep 2024, 13:54
Dans le programme officiel de spe maths, on parle d'approche intuitive de la notion de limite. Selon le niveau de la classe, tu peux tenter, dessins à l'appui...mais cette formalisation ne me paraît pas accessible à la majorité des élèves d'une classe de terminale actuellement.
Pour mettre une image, vous pouvez aller sur
https://postimages.org/fr/Vous choisirez ce qu'ils appellent le lien direct (lien de la seconde ligne), que vous placerez entre les balises Img.


-
chombier
- Membre Irrationnel
- Messages: 1324
- Enregistré le: 19 Juil 2012, 18:35
-
 par chombier » 21 Sep 2024, 14:29
par chombier » 21 Sep 2024, 14:29
Je sais, le programme de lycée est une catastrophe. Formaliser la notion de dérivée à partir d'une approche intuitive de la notion de limite. Donner une formule toute faite pour la dérivée d'une somme sans avoir les outils pour la démontrer...
Utiliser le TVI sur des intervalles de la forme

alors que dans l'énoncé du théorème, il est très clairement spécifié qu'il ne s'applique que sur des segments...
Comment leur donner le goût de la rigueur avec ça ?

-
vam
- Admin
- Messages: 681
- Enregistré le: 09 Aoû 2019, 09:50
-
 par vam » 21 Sep 2024, 14:36
par vam » 21 Sep 2024, 14:36
Oui, je sais...dur dur...
et pourquoi pas prendre la solution que je donnais à 13h32 ?
Pour mettre une image, vous pouvez aller sur
https://postimages.org/fr/Vous choisirez ce qu'ils appellent le lien direct (lien de la seconde ligne), que vous placerez entre les balises Img.


-
chombier
- Membre Irrationnel
- Messages: 1324
- Enregistré le: 19 Juil 2012, 18:35
-
 par chombier » 21 Sep 2024, 14:49
par chombier » 21 Sep 2024, 14:49
vam a écrit:Bonjour
Bon, un élève qui rédigera ça comme ça, aura ses points, OK
Mais je pense, une fois qu'on a vu dans quel secteur cela était possible, il n'est pas interdit de prendre de prendre deux valeurs du genre 0 et 2, de dire avant 0 rien, après 2 rien non plus, et de mettre en valeur f(0) et f(2). Et là on peut appliquer plus proprement. Non ?
Entre f(0) et f(2), ça fonctionne, mais je ne sais rien de f(2)
Si y=2,9999, je dois trouver un x>0 tel que f(x)>=2,9999
Ceci dit le "si ça tends vers 3, ça doit dépasser 2,9999 à un moment ou à un autre" est peut-être la formulation que je cherchais...
-
catamat
- Habitué(e)
- Messages: 1369
- Enregistré le: 07 Mar 2021, 10:40
-
 par catamat » 21 Sep 2024, 15:22
par catamat » 21 Sep 2024, 15:22
Bonjour
Pour avoir enseigné en TS il y a quelques années, on pouvait aussi utiliser le théorème de la bijection (après étude des variations)
Théorème de la bijection
Si f est continue et strictement monotone sur un intervalle I alors :
f réalise une bijection de l’intervalle I sur l’intervalle f (I).
Dans ce théorème I peut être ouvert ou semi ouvert.
Cela sous entend bien sûr de savoir déterminer l'image d'un intervalle.
voir parex:
https://www.educastream.com/fr/theoreme ... erminale-s

-
chombier
- Membre Irrationnel
- Messages: 1324
- Enregistré le: 19 Juil 2012, 18:35
-
 par chombier » 21 Sep 2024, 15:34
par chombier » 21 Sep 2024, 15:34
catamat a écrit:Bonjour
Pour avoir enseigné en TS il y a quelques années, on pouvait aussi utiliser le théorème de la bijection (après étude des variations)
Théorème de la bijection
Si f est continue et strictement monotone sur un intervalle I alors :
f réalise une bijection de l’intervalle I sur l’intervalle f (I).
Dans ce théorème I peut être ouvert ou semi ouvert.
Cela sous entend bien sûr de savoir déterminer l'image d'un intervalle.
voir parex:
https://www.educastream.com/fr/theoreme ... erminale-s
Ah il est très bien celui là, je l'adopte !
D'autant qu'en terminale, on n'utilise quasiment que le théorème de la bijection

Merci

Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 25 invités


