Bonjour, Merci de m'aider
-4 cos² x + 2(V3-1) sin x +4 - V3 =0
Trigo
7 messages
- Page 1 sur 1
Re: trigo
bonjour,
est ce que je pars sur le bon principe ?
-4 cos² x + 2 (racine3 -1) sin x + 4 - racine 3 = 0
= -3 - sin² x +2 (racine3 -1) sin x + 4 - racine 3 = 0
= - sin² x -1 (racine3 -1) sin x + 4 - racine 3 = 0
je suis perdue
est ce que je pars sur le bon principe ?
-4 cos² x + 2 (racine3 -1) sin x + 4 - racine 3 = 0
= -3 - sin² x +2 (racine3 -1) sin x + 4 - racine 3 = 0
= - sin² x -1 (racine3 -1) sin x + 4 - racine 3 = 0
je suis perdue
Re: trigo
ou plutôt
-4 cos² x + 2 (racine3 -1) sin x + 4 - racine 3 = 0
= -3 - sin² x +2 (racine3 -1) sin x + 4 - racine 3 = 0
= -sin ² x +2 (racine 3 -1) sin x +1 - racine 3 = 0
= sin² x +2(racine 3 - 1) - sin x+1 - racine 3= 0
= 3sin x + 1 ( 1-racine 3²)
j'ai l'impression de tout mélanger
-4 cos² x + 2 (racine3 -1) sin x + 4 - racine 3 = 0
= -3 - sin² x +2 (racine3 -1) sin x + 4 - racine 3 = 0
= -sin ² x +2 (racine 3 -1) sin x +1 - racine 3 = 0
= sin² x +2(racine 3 - 1) - sin x+1 - racine 3= 0
= 3sin x + 1 ( 1-racine 3²)
j'ai l'impression de tout mélanger
Re: trigo
bjr
-4 cos² x + 2(V3-1) sin x +4 - V3 =0
-4 cos² x + 4+ 2(V3-1) sin x - V3 =0
4(1- cos² x) + 2(V3-1) sin x - V3 =0
4sin²x + 2(V3-1) sin x - V3 =0
tu poses y=sinx
et resoudre
4y²+2(V3-1) y - V3 =0
si tu preferes avec les X
4X²+2(V3-1)X - V3 =0
-4 cos² x + 2(V3-1) sin x +4 - V3 =0
-4 cos² x + 4+ 2(V3-1) sin x - V3 =0
4(1- cos² x) + 2(V3-1) sin x - V3 =0
4sin²x + 2(V3-1) sin x - V3 =0
tu poses y=sinx
et resoudre
4y²+2(V3-1) y - V3 =0
si tu preferes avec les X
4X²+2(V3-1)X - V3 =0
Re: trigo
ah je n'y étais pas du tout. Merci
et pour construire les extrémités sur le cercle trigonométrique?
et pour construire les extrémités sur le cercle trigonométrique?
Re: trigo
l'équation du second degré (d'inconnue le sinus) a pour solutions:
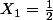 et
et 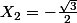
(le Delta vaut
^2+4 \sqrt{3})=4(\sqrt{3}+1)^2) )
)
il reste à résoudre les deux équations:
=\frac{1}{2}) et
et =-\frac{\sqrt{3}}{2})
(le Delta vaut
il reste à résoudre les deux équations:
7 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 33 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
