Tribu engendrée par l'ensemble des parties finies d'un ensemble
16 messages
- Page 1 sur 1
Tribu engendrée par l'ensemble des parties finies d'un ensemble
Bonjour,
Je suis bloqué sur un problème censé être très simple :
-Quelle est la tribu engendrée par l'ensemble des parties finies de X ?
(où X est un ensemble quelconque).
L'ensemble de parties formé par :
-L'ensemble vide
-X
-L'ensemble des parties finies de X
-Les complémentaires dans X des parties en question
n'est pas une tribu car les unions dénombrables de parties finies ne sont pas nécessairement finies.
On peut donc imager de prendre :
-L'ensemble vide
-X
-L'ensemble des parties dénombrables de X
-Les complémentaires dans X des parties en question
qui est bien une tribu et contient bien l'ensemble des parties finies de X.
Mais est-ce la plus petite tribu contenant l'ensemble des parties finies de X ? Si oui, comment le démontrer ?
Merci d'avance pour votre aide..
Je suis bloqué sur un problème censé être très simple :
-Quelle est la tribu engendrée par l'ensemble des parties finies de X ?
(où X est un ensemble quelconque).
L'ensemble de parties formé par :
-L'ensemble vide
-X
-L'ensemble des parties finies de X
-Les complémentaires dans X des parties en question
n'est pas une tribu car les unions dénombrables de parties finies ne sont pas nécessairement finies.
On peut donc imager de prendre :
-L'ensemble vide
-X
-L'ensemble des parties dénombrables de X
-Les complémentaires dans X des parties en question
qui est bien une tribu et contient bien l'ensemble des parties finies de X.
Mais est-ce la plus petite tribu contenant l'ensemble des parties finies de X ? Si oui, comment le démontrer ?
Merci d'avance pour votre aide..
effectivement..
Il paraît, en effet.. mais comment démontre-t-on le caractère "plus petit" (contenant) ?
Tu prends une autre tribu qui contient les singletons et tu vérifies que la tribu que tu as trouvé y est incluse.
Pour ça tu prend un élément de ta "tribu engendré" , tu le relies aux singletons par une propriété pour laquelle les tribus sont stable et comme l'autre tribu contient aussi les singletons, elle contiendra cet élément.
Pour ça tu prend un élément de ta "tribu engendré" , tu le relies aux singletons par une propriété pour laquelle les tribus sont stable et comme l'autre tribu contient aussi les singletons, elle contiendra cet élément.
Proposition de démo
Bon, alors j'essaie :
Notons F(X) l'ensemble des parties finies de X.
Soit A la tribu contenant toutes les parties dénombrables de X et leurs compléments (en particulier, on a bien et X dans A).
et X dans A).
Montrons que A est la plus petite tribu contenant F(X).
Soit B une tribu contenant F(X) ; montrons que B contient A.
Soit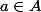 ; montrons que
; montrons que 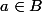 .
.
Par définition de A, on peut écrire a comme l'union dénombrable de parties dénombrables de X jointe à l'union dénombrable de complémentaires de parties dénombrables de X :
En clair, il existe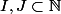 et des ensembles
et des ensembles 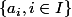 et
et 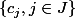 tels que les
tels que les 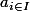 et les
et les 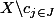 soient des parties dénombrables de X vérifiant :
soient des parties dénombrables de X vérifiant :
\cup\left(\bigcup_{j\in J}c_{j}\right)) .
.
Les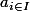 et les
et les 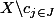 étant dénombrables, on peut les découper en unions dénombrable de singletons et écrire
étant dénombrables, on peut les découper en unions dénombrable de singletons et écrire \right)\cup\left(\bigcup_{j\in J}X\backslash\left(\bigcup_{y\in X\backslash c_{j}}\left\{ y\right\} \right)\right)) où toutes les unions sont dénombrables.
où toutes les unions sont dénombrables.
Comme B contient F(X), B contient toutes les parties finies de X (et en particulier les singletons) ; et comme B est une tribu, il contient donc toutes les unions dénombrables de singletons de X.
L'union de singletons définissant a étant dénombrable, on a bien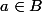 .
.
En conclusion, B contient A et donc A est la plus petite tribu contenant F(X) - c'est à dire la tribu engendrée par F(X).
Notons F(X) l'ensemble des parties finies de X.
Soit A la tribu contenant toutes les parties dénombrables de X et leurs compléments (en particulier, on a bien
Montrons que A est la plus petite tribu contenant F(X).
Soit B une tribu contenant F(X) ; montrons que B contient A.
Soit
Par définition de A, on peut écrire a comme l'union dénombrable de parties dénombrables de X jointe à l'union dénombrable de complémentaires de parties dénombrables de X :
En clair, il existe
Les
Comme B contient F(X), B contient toutes les parties finies de X (et en particulier les singletons) ; et comme B est une tribu, il contient donc toutes les unions dénombrables de singletons de X.
L'union de singletons définissant a étant dénombrable, on a bien
En conclusion, B contient A et donc A est la plus petite tribu contenant F(X) - c'est à dire la tribu engendrée par F(X).
Les éléments de A sont de deux types :
Ceux qui sont dénombrables.
Ceux dont le complémentaire dans X est dénombrable.
Je trouve que de dire qu'un élément de A est une réunion dénombrable de parties dénombrables de X et de complémentaires de parties dénombrables de X est incroyablement et inutilement compliqué.
Avant, tu as bien montré que A était une tribu ?
Ceux qui sont dénombrables.
Ceux dont le complémentaire dans X est dénombrable.
Je trouve que de dire qu'un élément de A est une réunion dénombrable de parties dénombrables de X et de complémentaires de parties dénombrables de X est incroyablement et inutilement compliqué.
Avant, tu as bien montré que A était une tribu ?
Je serais ravi de lire votre solution plus simple..
J'ai pu faire une erreur de raisonnement, mais voici ce à qui je pensais :
A est la tribu qui contient les parties dénombrables de X, leurs complémentaires, et toutes les combinaisons qu'on peut en faire par union dénombrable.
Justification :
-L'union de deux parties dénombrables est dénombrable
-L'union de deux complémentaires de parties dénombrables est le complémentaire d'une partie dénombrable (soient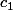 et
et 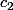 deux parties dénombrables de X ; on a
deux parties dénombrables de X ; on a ) ; et
; et 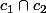 est dénombrable)
est dénombrable)
-Si on considère une union mixte du type dénombrable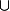 complémentaire de dénombrable (notés respectivement
complémentaire de dénombrable (notés respectivement  et
et 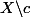 ), le complémentaire de cette union est
), le complémentaire de cette union est \cap c) qui est également une union mixte car les complémentaires de a et de X\c sont également compris dans A par définition de ce dernier.
qui est également une union mixte car les complémentaires de a et de X\c sont également compris dans A par définition de ce dernier.
+ avec généralisation aux unions dénombrables par récurrence
J'ai pu faire une erreur de raisonnement, mais voici ce à qui je pensais :
A est la tribu qui contient les parties dénombrables de X, leurs complémentaires, et toutes les combinaisons qu'on peut en faire par union dénombrable.
Justification :
-L'union de deux parties dénombrables est dénombrable
-L'union de deux complémentaires de parties dénombrables est le complémentaire d'une partie dénombrable (soient
-Si on considère une union mixte du type dénombrable
+ avec généralisation aux unions dénombrables par récurrence
une précision..
Je présume qu'un ensemble ne contenant que deux types de parties (dénombrables et complémentaire de dénombrable) ne serait pas une tribu dans le cas général car toute union mixte sortirait de l'ensemble (si X est choisi indénombrable par exemple).
(sauf erreur de ma part, l'union d'un ensemble dénombrable et d'un complémentaire de dénombrable est un ensemble indénombrable quelconque, pas forcément de l'un de ces deux types)
(sauf erreur de ma part, l'union d'un ensemble dénombrable et d'un complémentaire de dénombrable est un ensemble indénombrable quelconque, pas forcément de l'un de ces deux types)
Par définition de A, on peut écrire a comme l'union dénombrable de parties dénombrables de X jointe à l'union dénombrable de complémentaires de parties dénombrables de X :
C'est pas plutôt des unions dénombrables de partie finie (ou de singletons) que tu voulais prendre ?
Ce que dit Doraki, c'est que tu peux vérifier que ces deux classes d'éléments appartenant à A sont dans B. Après la stabilité par union permet de conclure plus rapidement.
D'ailleurs on peut le faire en une phrase à chaque fois, ça évite d'introduite des notations complexes.
Si
A partir de cette phrase, c'est clair par passage au complémentaire que l'autre type est dedans.
Et les unions mixte y sont aussi, par stabilité par union.
Certes..
Vous avez raison, en fait c'est mon tout premier post qui était erroné.
Le A que j'ai pris coïncide bien avec la tribu engendrée par les singletons (et les parties dénombrables suivent par union dénombrable).
Êtes-vous d'accord avec cette affirmation ?
Je vais essayer de rédiger quelque chose de plus propre sur la base de vos recommandations.. merci !
Le A que j'ai pris coïncide bien avec la tribu engendrée par les singletons (et les parties dénombrables suivent par union dénombrable).
Êtes-vous d'accord avec cette affirmation ?
Je vais essayer de rédiger quelque chose de plus propre sur la base de vos recommandations.. merci !
mmestre a écrit:A est la tribu qui contient les parties dénombrables de X, leurs complémentaires, et toutes les combinaisons qu'on peut en faire par union dénombrable.
Les combinaisons qu'on peut en faire sont AUSSI des parties dénombrables ou de complémentaire dénombrable.
L'ensemble des parties dénombrables et de complémentaire dénombrable est DEJA une tribu.
Essai de démo propre
On reprend.
Je prends A la tribu engendrée par les singletons de X (c'est une tribu par définition).
Je prends une autre tribu B contenant F(X), et je veux montrer que B contient A (ce qui montrera que A est aussi la tribu engendrée par F(X) car c'est la plus petite tribu contenant ce dernier).
1) Soit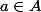 supposé dénombrable. On peut écrire
supposé dénombrable. On peut écrire  comme l'union (dénombrable) des singletons formés par ses éléments.
comme l'union (dénombrable) des singletons formés par ses éléments.
 est donc un élément de B en raison du fait que B est une tribu contenant les parties finies de X (donc en particulier les singletons et toute union dénombrable de ceux-ci).
est donc un élément de B en raison du fait que B est une tribu contenant les parties finies de X (donc en particulier les singletons et toute union dénombrable de ceux-ci).
2) Soit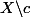 supposé complémentaire dans
supposé complémentaire dans  d'un dénombrable
d'un dénombrable  .
.
On peut écrire comme l'union (dénombrable) des singletons formés par ses éléments.
comme l'union (dénombrable) des singletons formés par ses éléments.
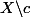 est donc un élément de B en raison du fait que B est une tribu contenant les parties finies de X (donc en particulier les singletons et le complémentaire de toute union dénombrable de ceux-ci).
est donc un élément de B en raison du fait que B est une tribu contenant les parties finies de X (donc en particulier les singletons et le complémentaire de toute union dénombrable de ceux-ci).
On peut maintenant considérer une union dénombrable constituée d'éléments de type 1) et 2) ; cette union sera un élément de B car c'est le cas pour chaque élément de ces deux types, et en utilisant la propriété de stabilité par union de la tribu B.
Est-ce plus proche de ce que vous préconisiez ?
---
À ce propos, quelle est la justification de votre affirmation "Les combinaisons qu'on peut en faire sont AUSSI des parties dénombrables ou de complémentaire dénombrable." ? Ça ne me saute pas aux yeux..
Je prends A la tribu engendrée par les singletons de X (c'est une tribu par définition).
Je prends une autre tribu B contenant F(X), et je veux montrer que B contient A (ce qui montrera que A est aussi la tribu engendrée par F(X) car c'est la plus petite tribu contenant ce dernier).
1) Soit
2) Soit
On peut écrire
On peut maintenant considérer une union dénombrable constituée d'éléments de type 1) et 2) ; cette union sera un élément de B car c'est le cas pour chaque élément de ces deux types, et en utilisant la propriété de stabilité par union de la tribu B.
Est-ce plus proche de ce que vous préconisiez ?
---
À ce propos, quelle est la justification de votre affirmation "Les combinaisons qu'on peut en faire sont AUSSI des parties dénombrables ou de complémentaire dénombrable." ? Ça ne me saute pas aux yeux..
Ce que disait Nightmare, c'est que si une tribu A est engendrée par un ensemble S, et si on a une tribu B (dans ton cas, la tribu engendrée par les singletons),
A est inclus dans B S est inclus dans B.
A est par définition la plus petite tribu contenant S.
Donc si tu montres que B contient S (i.e. les ensembles dénombrables et codénombrables), t'as fini. Tu n'as jamais besoin de parler des trucs compliqués que tu peux avoir dans A.
Dans ton 1er post, tu dis que A = l'ensemble des parties dénombrables ou codénombrables est une tribu :
Mais ça a l'air de beaucoup te surprendre, donc tu ne l'as jamais montré ?
Une union dénombrable d'ensembles dénombrables est toujours un ensemble dénombrable.
L'intersection d'un ensemble dénombrable avec un ensemble quelconque est toujours un ensemble dénombrable.
Et quand on passe au complémentaire :
Une intersection dénombrable d'ensembles codénombrables est toujours un ensemble codénombrable.
La réunion d'un ensemble codénombrable avec un ensemble quelconque est toujours un ensemble codénombrable.
A est inclus dans B S est inclus dans B.
A est par définition la plus petite tribu contenant S.
Donc si tu montres que B contient S (i.e. les ensembles dénombrables et codénombrables), t'as fini. Tu n'as jamais besoin de parler des trucs compliqués que tu peux avoir dans A.
Dans ton 1er post, tu dis que A = l'ensemble des parties dénombrables ou codénombrables est une tribu :
mmestre a écrit:On peut donc imager de prendre :
-L'ensemble vide
-X
-L'ensemble des parties dénombrables de X
-Les complémentaires dans X des parties en question
qui est bien une tribu et contient bien l'ensemble des parties finies de X.
Mais ça a l'air de beaucoup te surprendre, donc tu ne l'as jamais montré ?
Une union dénombrable d'ensembles dénombrables est toujours un ensemble dénombrable.
L'intersection d'un ensemble dénombrable avec un ensemble quelconque est toujours un ensemble dénombrable.
Et quand on passe au complémentaire :
Une intersection dénombrable d'ensembles codénombrables est toujours un ensemble codénombrable.
La réunion d'un ensemble codénombrable avec un ensemble quelconque est toujours un ensemble codénombrable.
Les combinaisons qu'on peut en faire sont AUSSI des parties dénombrables ou de complémentaire dénombrable.
SI tu veux vérifier ça, une union dénombrable de dénombrables est dénombrable. Et si l'un des élt de l'union est de complémentaire dénombrable, alors l'union sera de complémentaire dénombrable.
Tu peux t'en servir aussi, c'est plus malin à haut niveau mais si tu débutes et que tu galères pour le montrer... Dans tous les cas, il faut au moins le faire pour comprendre pourquoi c'est vrai et mieux appréhender la notion abstraite de tribu.
A est par définition la plus petite tribu contenant S.
N'étais-ce pas ce qu'il fallait montrer ?
Merci !
Merci beaucoup à vous deux pour ces précisions, c'est effectivement la "clé" qui me manquait.
Mon livre d'intégration (Pagès) démontrait bien sûr que l'union dénombrables d'ensembles dénombrables est dénombrable, mais je n'avais pas vu (et de fait, j'ai l'impression qu'elle n'y figure pas) la proposition pour l'intersection.
Forcément, j'imagine que ces considérations sur les ensembles dénombrables sont des rappels de premier cycle..
Donc bien sûr l'union d'un codénombrable avec un ensemble quelconque est codénombrable, et ça résoud mon problème :)
Si je ne m'abuse, l'argument à invoquer est que tout sous-ensemble d'un dénombrable est dénombrable ?
(l'intersection produisant un sous-ensemble des deux ensembles en intersection).
Mon livre d'intégration (Pagès) démontrait bien sûr que l'union dénombrables d'ensembles dénombrables est dénombrable, mais je n'avais pas vu (et de fait, j'ai l'impression qu'elle n'y figure pas) la proposition pour l'intersection.
Forcément, j'imagine que ces considérations sur les ensembles dénombrables sont des rappels de premier cycle..
Donc bien sûr l'union d'un codénombrable avec un ensemble quelconque est codénombrable, et ça résoud mon problème :)
Si je ne m'abuse, l'argument à invoquer est que tout sous-ensemble d'un dénombrable est dénombrable ?
(l'intersection produisant un sous-ensemble des deux ensembles en intersection).
16 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 35 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
