Bonjour à tous, je suis bloqué sur un exercice sur les transformations de Fourier et les reps de groupes..
Voici l'énoncé :
Soit G un gp fini et

l'ensemble des classes d'équivalences de ses représentations irréductibles complexes (de dim finie donc).
Pour chaque

on choisit une représentation
)
dans la classe i.
On définit le coefficient de Fourier
)
de
)
par :
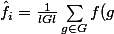R^i(g))
Et voici la question qui me pose problème :
Si
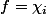
(le caractère de la représentation
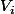
), montrer que :
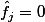
si

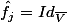
si
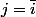
Une indication me dit de me servir d'une base orthonormée de
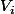
pour écrire éléments de la matrice

et ensuite d'utiliser les relations d'orthogonalité de Schur..
Mais honnetement cela ne m'aide pas..
Je vous remercie d'avoir lu et aussi de tenter de m'aider.

