Transformation d'Abel

[acoustica]

Bonjour,

Je m'remets doucement aux maths et je voudrais avoir quelques pistes de résolution pour une série classique :

Etudier la convergence de

J'ai réécris puis appliqué la transformation d'Abel :

Transformation d'Abel

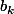
Le problème avec la transformation d'Abel, c'est de savoir laquelle des deux suites on prend pour (en prenant pour référence les notations du site en lien). J'ai pris la suite 1/k pour obtenir du 1/(k*(k+1)), en me disant que c'était équivalent à 1/k^2. Je ne sais déjà pas si c'est le bon choix.

Ne sachant pas trop quoi prendre, je l'ai appliquée deux fois pour obtenir d'une part :
avec

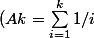et d'autre part :

en choisissant

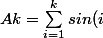Seulement, je ne vois laquelle des deux choisir. Pourriez-vous me donner un coup de main ? Merci !

[raito123]

Bonjour Acoustica :)

Je ne vois pas trop comment tu peux majorer la série harmonique ... et pus y a une seule suite ( parmi sin(n) et 1/n ) qui est décroissante et qui tend vers 0 !!!

j’espère que cela t'aide pour trouver qui est quoi :p

PS : le lien ne marche pas

[acoustica]

Bonjour Acoustica

Je ne vois pas trop comment tu peux majorer la série harmonique ... et pus y a une seule suite ( parmi sin(n) et 1/n ) qui est décroissante et qui tend vers 0 !!!

j’espère que cela t'aide pour trouver qui est quoi :p

PS : le lien ne marche pas

Yop coucou Raito !

Oui, justement c'est un peu mon souci. Puisqu'a priori je me détourne de la première option, et je choisis pour Ak la série des sin(k). Je peux majorer par k, ce qui me permet de majorer ce qui me fait retomber sur le même problème : majorer la série harmonique.

[Arkhnor]

Bonjour,

Si tu majores ta somme de sinus aussi brutalement, tu n'aboutiras à rien. C'est une somme oscillante : le sinus oscille autour de 0, et donc les termes se compensent entre eux pour au final avoir une somme relativement petite. Si tu majores la valeur absolue de la somme par la somme des valeurs absolues, tu détruit complètement ce phénomène.

Calcule explicitement ce que vaut la somme des sinus de 1 à n. (passe à la formulation exponentielle, et utilise la formule qui donne la somme des termes d'une suite géométrique)

[acoustica]

Yop coucou Raito !

Oui, justement c'est un peu mon souci. Puisqu'à priori je me détourne de la première option, et je choisis pour Ak la série des sin(k). Je peux majorer par k, ce qui me permet de majorer ce qui me fait retomber sur le même problème : majorer la série harmonique.

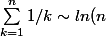En fait, je devrais y aller pas-à-pas. Déjà, j'ose pas écrire des trucs comme . Je confonds équivalents, développement asymptotique... Là, on ne va pas utiliser d'équivalents n'est-ce pas ?

[acoustica]

Bonjour,

Si tu majores ta somme de sinus aussi brutalement, tu n'aboutiras à rien. C'est une somme oscillante : le sinus oscille autour de 0, et donc les termes se compensent entre eux pour au final avoir une somme relativement petite. Si tu majores la valeur absolue de la somme par la somme des valeurs absolues, tu détruit complètement ce phénomène.

Calcule explicitement ce que vaut la somme des sinus de 1 à n. (passe à la formulation exponentielle, et utilise la formule qui donne la somme des termes d'une suite géométrique)

Bonjour,
Oui je vois l'idée. Merci ! Je vais voir si je peux conclure.

[raito123]

Bonjour,
Oui je vois l'idée. Merci ! Je vais voir si je peux conclure.

Oui c'est ce qu'il fallait faire

[raito123]

Si je peux me permettre : on utilise souvent le théorème d'Abel en le combinant avec le critère de Cauchy :)

[acoustica]

Si je peux me permettre : on utilise souvent le théorème d'Abel en le combinant avec le critère de Cauchy

Ah oui, je vois, avec le bk-b-(k+1), c'est ça ?

Si je reprends l'exercice, je me retrouve à étudier la convergence de la série :

. C'est bien ça ?
Mais on retombe sur le même type de série ! On refait une transformation d'Abel ?

[raito123]

Montrer la convergence d'une série équivaut à montrer que la somme partielle vérifie le critère de Cauchy ... et pour celà on utilise la transformation d'Abel si les conditions sont satisfait !!

C'est le cas pour ta série :)

[acoustica]

Montrer la convergence d'une série équivaut à montrer que la somme partielle vérifie le critère de Cauchy ... et pour celà on utilise la transformation d'Abel si les conditions sont satisfait !!

C'est le cas pour ta série

Ah ok ! Je vois je vois. Alors oui, de ce point de vue, c'est pas bon ce que je viens de faire. Bon, je vais recommencer depuis le début, en tenant compte du critère de Cauchy. Si j'ai un problème, je reviendrai. Merci beaucoup à toi en tout cas !

[raito123]

Mais pas de quoi :zen:

[acoustica]

Pour ceux qui tomberaient sur le fil et qui veulent des explications claires :

http://gilles.costantini.pagesperso-orange.fr/prepas_fichiers/abel.pdf

Appliqué à la série sin(n)/n, on choisit la suite 1/n pour . On prouve que la série partielle des sin(n) est majorée (passage aux complexes et majoration de la partie imaginaire de la somme).


Et ça, ça n'a aucun rapport, mais c'est joli :
http://www.youtube.com/watch?v=cjV4Q5sR9c8&feature=related