Trace d'une extension galoisienne
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 09 Déc 2010, 19:09
par Nightmare » 09 Déc 2010, 19:09
Salut,
On me demande de montrer que si
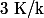
est galoisienne alors
\;\; =\; \Bigsum_{\sigma \in Gal(K/k)}\; \sigma(x))
quel que soit x dans K.
Ca se fait facilement à la main en utilisant la décomposition du polynôme minimal de x à l'aide de ses conjugués, mais l'exercice propose en indication d'utiliser un résultat d'un exercice précédent (que je n'ai pas encore traité), à savoir que si K/k est galoisienne alors
}\; K)
(en tant que k-algèbre)
Moi qui comptait m'attaquer aux révision du produit tensoriel demain, j'aimerais donc comprendre cette indication (que je trouve du coup vachement compliquée par rapport au gabarit de la preuve à la main) mais j'avoue ne pas y voir grand chose. Dans un premier temps, que signifie la notation
} K)
? Je verrai ensuite une fois ceci éclairci si j'arrive à utiliser cette indication.
Merci pour vos lumières.
:happy3:
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 09 Déc 2010, 19:50
par Doraki » 09 Déc 2010, 19:50
Je suis pas sûr de comprendre comment
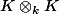
est une k-algèbre.
 \times (c \otimes d) = (a \times c) \otimes (b \times d))
?
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 09 Déc 2010, 19:57
par Nightmare » 09 Déc 2010, 19:57
Hello,
ben, le produit tensoriel de deux k-algèbre est toujours une k-algèbre avec la lci
(x_{2}\otimes_{k} y_{2})=(x_{1}x_{2})\otimes_{k} (y_{1}y_{2}))
non?
Il me semble même bien qu'ici le produit tensoriel peut être vu comme une K-algèbre.
Edit : pas vu ton édit
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 09 Déc 2010, 20:01
par Doraki » 09 Déc 2010, 20:01
ok, et l'isomorphisme de k-algèbres, c'est bien le truc qui prolonge
 -> \Bigoplus_{g \in Gal(K/k)} x g(y))
(j'ai pas vérifié que c'était un isomorphisme mais chuis tenté de penser que c'en est un)
La "somme directe" de k-algèbres, c'est simplement n copies de K, où l'addition et les multiplications interne et externe se font composante par composante.
Dans ce cas il suffirait de dire genre que la trace est conservée par l'extension des scalaires, et donc que la trace de la multiplication par
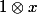
, quand on l'écrit dans la K-base donnée par le truc à droite, ben c'est pile ce qu'il faut ?
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 09 Déc 2010, 20:14
par Nightmare » 09 Déc 2010, 20:14
Ah !! Je crois que j'ai ... tout compris ! (c'est rare).
Ton truc est bien un isomorphisme (c'est dû à l'indépendance linéaire des caractères).
Du coup, la somme des sigma(x) est la trace de l'application K-linéaire qui multiplie chaque facteur par sigma(x) sur la K-algèbre
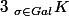
. par notre isomorphisme, c'est aussi la trace de la multiplication par x de chaque facteur de droite sur la K-algèbre K tenseur K et la trace ne dépendant pas du corps de base, on a ce qu'on veut.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 59 invités
