Ncdk a écrit:Du coup je pense à autre chose, en gros prendre a et b entiers et montrer que c ne l'est pas non ?
Heuuu... tu déconne ou quoi ?
Les
affixes a,b,c des points A,B,C, c'est des
complexes et le fait que A,B,C soient à coordonnées entières, ça veut évidement pas dire que a,b,c sont des entiers, mais que ce sont des "entiers de Gauss", c'est à dire des complexes de la forme x+iy avec x et y des entiers.
Après, bien sûr, on peut faire de l'arithmétique (avec des nombres premiers, des pgcd, etc...) sur les entiers de Gauss comme sur les entiers "normaux", mais vu que ça résulte du fait que Z[i] est Euclidien ce qui est tout sauf trivial (Z[omega] est rarement euclidien), c'est pas du tout du tout niveau Lycée de faire de l'arithmétique là dessus.
Bref, niveau Lycée, si tu part de cette relation pour caractériser les triangles équilatéraux, ben ce qu'il faut montrer, c'est qu'il n'y a pas de solution non triviales (i.e. avec a,b,c distincts) à l'équation a²+b²+c²=ab+bc+ca où a,b,c sont des complexes de la forme x+iy avec x et y entiers.
C'est évidement faisable, mais, tout aussi évidement, c'est bien plus compliqué que montrer directement que
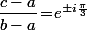
n'a pas de solution avec a,b,c de la forme x+iy ; x et y entiers : là, tu obtient en une ligne que, s'il y avait des solutions, ça signifierais que

est rationnel ce qui est faux.


