Théorème spectral

[Obito31]

bonsoir,
je bloque sur cette question :
Donner une démonstration directe du théorème spectral pour les endomorphismes autoadjoints
d’un espace hermitien de dimension 2 en calculant les projecteurs sur les espaces propres.

j'ai eu une petite idée mais fausse à coup sûr.
déjà le polynôme caractéristique admet au moins une racine, on s’intéresse au cas où on a qu'un espace propre de dimension 1 car sinon c'est trivial comme on est en dimension 2.
soit F ce sous espace, comme l'application est autoadjoint on a que f(F) orthogonal est inclus dans F orthogonal de plus que E = F ortho + F (somme direct) donc F ortho est de dimension 1
on a alors puisque que F ortho est stable par f et que F ortho est de dim 1 que F ortho un espace propre.
Déjà faut montré que F ortho est non nul.. aussi j'ai pas utiliser les projecteurs..

[aviateur]

Bonjour
Dans ce genre de question on ne sait jamais de quoi on peut partir.
Je suppose que tu sais démontrer que les vp sont réelles...
Si les 2 vp sont différentes, notons les des vecteurs propres correspondants de norme 1.
E_i,=1,2 les sev propres correspondant
Posons et

Pour tout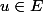 on a
par Cayley Hamilton

Ce qui montre que De plus si 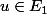on
a . Ce qui montrer que est le projecteur sur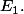
Idem en remplaçant i=1 par i=2.
On vérifie facilement l'égalité .
D'où la décomposition spectrale de f:
A noter qu'on peut écrire aussi Cela se vérifie aisément

[Obito31]

Bonjour aviateur et merci pour ta réponse.
Je ne comprend pas pourquoi tu suppose qu'il y a 2 valeur propre, si il y on a 2 alors l'espace peut se décomposer en somme directe de 2 espace propre de dimension 1 et donc f est diagonalisable non ?