Bonsoir,
Il semble que le théorème veuille dire:
le polynome est reductible ssi
il se factorise.
En développant la factorisation et en identifiant les coefficients
des différents produits d'indéterminées, les coefficients initiaux

sont des expressions polynomiales des coefficients

des polynômes facteurs.
On arrive à éliminer les

et démontrer que les
coefficients

sont algébriques.
ça a l'air diifficile mais pas surhumain (avec des résolvants)
de montrer l'existence de telle relations portant sur les coefficients

Par contre, la réciproque est-elle plus difficile, car il faut obtenir
une factorisation en ayant comme hypothèses
des relations algébriques

sur les coefficients qui n'ont peut-être rien à voir entre elles.
Alors, là ce qui peut se passer, c'set qu'avec la donnée d'une famille
de polynômes

quelconques,
les polynômes

vérifient des identités remarquables (des contraintes) tout à fait générales , en fait quasiment tautologiques, qui permettraient d'obtenir la factorisation.
Comme exemple, j'essayerai de regarder ce qui se passe pour des polynomes
comme
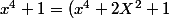-2x^2)
qui fait apparaitre un coefficient

dans

alors que sûrement il y a des corps Z/pZ
qui n'ont pas de racine de 2.
j'ai une autre idée,p-e absurde:
ça a l'air d'être un théorème d'une extrême généralité.Est-ce qu'ils parlent de catégories et d'élements universels dans ces catégories ?
, we consider the equation :
and
.