c'est ça non ? :hum:
Théorème de Noether
31 messages
- Page 2 sur 2 - 1, 2
Je pense que oui, mais en fait, je ne sait pas : il manque le théorème "B1" parlant de racines communes à tout un tas de polynômes.barbu23 a écrit:Bonjour Ben : :happy3:
Est ce que dans le concret , ce théorème est applicable, vue le nombre et la complexité du système à résoudre ! en plus ce n'est pas un système linéaire à resoudre mais non lineaire ! :happy3:
Merci d'avance ! :happy3:
Or, je ne connais (à peu prés) que la notion de résultant de DEUX polynômes et je ne vois à priori pas comment généraliser à plus de deux...
(le résultant est, quand à lui, tout ce qu'il y a de plus 'calculable' : c'est un (gros) déterminant)
Si tu précise un peu plus les références :
j'aurais peut-être le temps de jeter un coup d'oeuil...barbu23 a écrit:...danset
...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
re,
c'est un théorème extra(ordinaire) , non ?
Ils disent que les polynomes ne dépendent que de n et de d.
ne dépendent que de n et de d.
A la limite, celui qui a compris le théorème peut écrire un programme
informatique avec par exemple n=3 (3 indéterminées) et d=3 (on ne dépasse pas des polynômes de degré total de 3)
et sortir la liste effective de ces fameux polynomes.
D'autant que ces polynômes sont à coefficients dans Z.
Et ensuite, on a une belle caractérisation géométrique si le corps de
base est topologique:
un polynôme est réductible si et seulement si ses coefficients sont algébriques et appartiennent à une certaines sous-variété de
sont algébriques et appartiennent à une certaines sous-variété de }})
conclusion: au fond , on aimerait bien les voir ces polynômes pour de petites valeurs de n et d.
On liste bien les polynômes de Tchebyshev...
C'est (un peu) le défaut de pédagogie de l'université françoise:
beaucoup d'abstraction et pas suffisamment de pratique.
c'est un théorème extra(ordinaire) , non ?
Ils disent que les polynomes
A la limite, celui qui a compris le théorème peut écrire un programme
informatique avec par exemple n=3 (3 indéterminées) et d=3 (on ne dépasse pas des polynômes de degré total de 3)
et sortir la liste effective de ces fameux polynomes.
D'autant que ces polynômes sont à coefficients dans Z.
Et ensuite, on a une belle caractérisation géométrique si le corps de
base est topologique:
un polynôme est réductible si et seulement si ses coefficients
conclusion: au fond , on aimerait bien les voir ces polynômes pour de petites valeurs de n et d.
On liste bien les polynômes de Tchebyshev...
C'est (un peu) le défaut de pédagogie de l'université françoise:
beaucoup d'abstraction et pas suffisamment de pratique.
En fait, j'ai eu la même idée que vous..regardons
si on considère deux indéterminées X et Y et du degré total 2

on peut se dire: c'est un trinome de la variable réelle x
+bY^2+eY+f)
on calcule le
^2-4a(bY^2+eY+f))
 +2Y(cd-2ae)+d^2 - 4af)
et là se dire:
Si Delta n'est pas un carré parfait, ça ne sera pas du polynôme
mais une expression avec des racines carrées. :hum:
On calcule donc le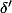 du
du  qu'on égalise à zéro.
qu'on égalise à zéro.
^2-(c^2-4ab)(d^2-4af)=0)
=0)
)
là , ce sont des coeffs a,b,c,d,e,f
en écrivant ça avec 6 indéterminées
)
on fait la même chose en Y,X, ce qui revient à permuter
a b
d e
)
)
ça a l'air à coefficients dans Z..
Pour faire le lien avec l'algèbre linéaire, il faudrait exprimer ces deux
polynomes comme des déterminants (de taille 4 ?)
Pour d=3 (degré 3) et n=3 (3 indéterminées), on peut essayer de faire la même chose avec les formules de Cardan.
si on considère deux indéterminées X et Y et du degré total 2
on peut se dire: c'est un trinome de la variable réelle x
on calcule le
et là se dire:
Si Delta n'est pas un carré parfait, ça ne sera pas du polynôme
mais une expression avec des racines carrées. :hum:
On calcule donc le
là , ce sont des coeffs a,b,c,d,e,f
en écrivant ça avec 6 indéterminées
on fait la même chose en Y,X, ce qui revient à permuter
a b
d e
ça a l'air à coefficients dans Z..
Pour faire le lien avec l'algèbre linéaire, il faudrait exprimer ces deux
polynomes comme des déterminants (de taille 4 ?)
Pour d=3 (degré 3) et n=3 (3 indéterminées), on peut essayer de faire la même chose avec les formules de Cardan.
Je pense que, pour le degrés 2, c'est exactement ça,
mais que, pour le degrés 3, c'est pas "toute" la méthode de cardan qu'on utilise (car il n'existe pas de telle méthode pour les degrés >4) mais (sans doute ?) seulement la notion de discriminant (qui elle existe quelque soit le degrés) qui est le résultant d'un polynôme et de sa dérivée.
On peut aussi dans le cas n=2 écrire la matrice (4x5) associée au système linéaire dont parle la preuve, puis les 5 sous déterminant 4x4 et essayer de comprendre comment, partant de ces 5 formes linéaires en a,b,c,d,e,f on peut obtenir ton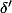 du cas n=d=2...
du cas n=d=2...
P.S. quand j'aurais un peu de temps, je regarderais, mais là, j'ai des copies pour demain sans fautes...
mais que, pour le degrés 3, c'est pas "toute" la méthode de cardan qu'on utilise (car il n'existe pas de telle méthode pour les degrés >4) mais (sans doute ?) seulement la notion de discriminant (qui elle existe quelque soit le degrés) qui est le résultant d'un polynôme et de sa dérivée.
On peut aussi dans le cas n=2 écrire la matrice (4x5) associée au système linéaire dont parle la preuve, puis les 5 sous déterminant 4x4 et essayer de comprendre comment, partant de ces 5 formes linéaires en a,b,c,d,e,f on peut obtenir ton
P.S. quand j'aurais un peu de temps, je regarderais, mais là, j'ai des copies pour demain sans fautes...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
31 messages
- Page 2 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 33 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
